
【题目】若关于![]() 的二次函数
的二次函数![]() (
(![]() 为常数)与
为常数)与![]() 轴交于两个不同的点
轴交于两个不同的点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其图象的顶点为点
,其图象的顶点为点![]() 是坐标原点.
是坐标原点.
(1)若![]() 、
、![]() 、
、![]() ,求此二次函数的解析式并写出二次函数的对称轴;
,求此二次函数的解析式并写出二次函数的对称轴;
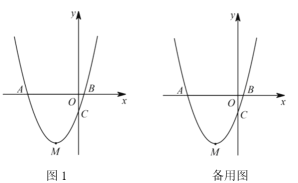
(2)如图1,若![]() ,
,![]() ,
,![]() 为直角三角形,
为直角三角形,![]() 是以
是以![]() 的等边三角形,试确定
的等边三角形,试确定![]() 的值;
的值;
(3)设![]() 为正整数,且
为正整数,且![]() ,
,![]() ,
,![]() 为任意常数,令
为任意常数,令![]() ,
,![]() ,如果对于一切实数
,如果对于一切实数![]() ,
,![]() 始终成立,求
始终成立,求![]() 的值.
的值.
【答案】(1)![]() ,对称轴
,对称轴![]() ;(2)
;(2)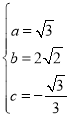 ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)函数的表达式为:y=a(x+2)(x-4)=a(x2-2x-8),即可求解;
(2)设![]() ,
,![]() ,
,![]() ,由
,由![]() ,得到
,得到![]() ,结合一元二次方程根与系数的关系,得到
,结合一元二次方程根与系数的关系,得到![]() ;由
;由![]() 为边长2的等边三角形,则
为边长2的等边三角形,则![]() ,得到
,得到![]() ;由
;由![]() ,得到
,得到![]() ,联立方程组,即可求出a、b、c的值.
,联立方程组,即可求出a、b、c的值.
(3)先表示出解析式,求出点A、B的横坐标,得到AB=x2-x1=|mt+3|≥|2t+n|,对于一切实数t,上式都成立,则必然存在|mt+3|=|2t+n|,结合一元二次方程根的判别式即可求解.
解:(1)设函数的表达式为:y=a(x+2)(x-4)=a(x2-2x-8),
把点C代入,则-8a=3,
解得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴对称轴![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,
,
∵![]() 为直角三角形,且
为直角三角形,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,
,![]() ,
,
则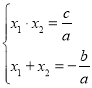 ,
,
∴![]() ,
,
∴![]() ①;
①;
又∵![]() 为边长2的等边三角形,
为边长2的等边三角形,
∴抛物线顶点坐标中纵坐标为![]() ,且
,且![]() .
.
∴![]() ,
,
∴![]() ②;
②;
又∵![]()
∴![]() ③
③
由①②③得: ,
,
解得: ;
;
(3)根据题意,解析式:![]() .
.
令![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴AB=![]() ;
;
∴![]() (两边平方),
(两边平方),
∴![]() ,
,
∴![]() ,
,
∴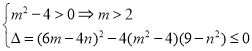 恒成立.
恒成立.
∴![]() ,
,
∴![]() 且
且![]() 为正整数
为正整数
∴![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】图①,图②均是![]() 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段
的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段![]() 的端点都在格点上,仅用无刻度的直尺完成如下作图,保留作图痕迹.
的端点都在格点上,仅用无刻度的直尺完成如下作图,保留作图痕迹.
(1)在图①中画一个钝角![]() ,且点
,且点![]() 在格点上,使它有一边与该边上的高线长度相等;
在格点上,使它有一边与该边上的高线长度相等;
(2)在图②中画一个五边形![]() ,使其是轴对称图形,且
,使其是轴对称图形,且![]() ,点
,点![]() 、
、![]() 、
、![]() 在格点上.
在格点上.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节是我国传统佳节,圆圆同学带了4个月饼(除馅不同外,其它均相同),其中有两个火腿馅月饼、一个蛋黄馅和一个枣泥馅月饼.
(1)请你根据上述描述,写出一个不可能事件.
(2)圆圆准备从中任意拿出两个送给她的好朋友月月.
①用树状图或列表的方法列出圆圆拿到两个月饼的所有可能结果;
②请你计算圆圆拿到的两个月饼都是火腿馅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,![]() ,
,![]() ,点P从A开始沿边AB向终点B以
,点P从A开始沿边AB向终点B以![]() 的速度移动,与此同时,点Q从点B开始沿边BC向终点C以
的速度移动,与此同时,点Q从点B开始沿边BC向终点C以![]() 的速度移动,如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动
的速度移动,如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动![]() 设运动时间为t秒.
设运动时间为t秒.
![]() 填空:
填空:![]() ________,
________,![]() ________
________![]() 用含t的代数式表示
用含t的代数式表示![]() :
:
![]() 当t为何值时,PQ的长度等于5cm?
当t为何值时,PQ的长度等于5cm?
![]() 是否存在t的值,使得五边形APQCD的面积等于
是否存在t的值,使得五边形APQCD的面积等于![]() ?若存在,请求出此时t的值;若不存在,请说明理由.
?若存在,请求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们越来越注重营养健康,有一种有机水果![]() 在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克
在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克![]() 水果,立即将其冷藏,请根据下列信息解决问题:
水果,立即将其冷藏,请根据下列信息解决问题:
①水果![]() 的市场价每天每千克上涨0.1元;
的市场价每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天;
(1)若将这批![]() 水果存放
水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为 元;
天后这批水果的销售单价为 元;
(2)将这批![]() 水果存放多少天后一次性出售所得利润为9600元?
水果存放多少天后一次性出售所得利润为9600元?
(3)将这批![]() 水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
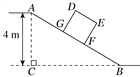
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生的视力状况受到社会的广泛关注,某市有关部门对全市3万名初中生的视力状况进行了一次抽样调查,下图是利用所得数据绘制的频数分布直方图,根据图中所提供的信息回答下列问题:
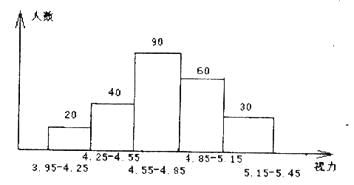
(1)本次调查共抽测了多少名学生?
(2)在这个问题中的样本指什么?
(3)如果视力在4.9-5.1(含4.9和5.1)均属正常,那么全市有多少名初中生视力正常?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )
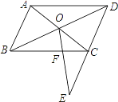
A. 1 B. 1.5 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.
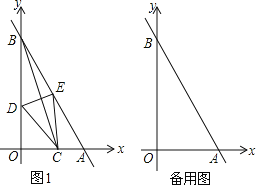
(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com