
【题目】初中生的视力状况受到社会的广泛关注,某市有关部门对全市3万名初中生的视力状况进行了一次抽样调查,下图是利用所得数据绘制的频数分布直方图,根据图中所提供的信息回答下列问题:
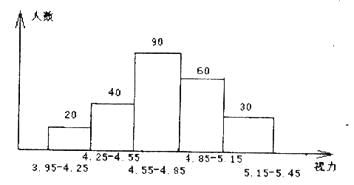
(1)本次调查共抽测了多少名学生?
(2)在这个问题中的样本指什么?
(3)如果视力在4.9-5.1(含4.9和5.1)均属正常,那么全市有多少名初中生视力正常?
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,点E为CD上一点,AE,BE分别平分∠DAB,∠CBA.

(1)求证:AE⊥BE;
(2)求证:DE=CE;
(3)若AE=4,BE=6,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,0),B(0,3),过点B画y轴的垂线l,点C在线段AB上,连结OC并延长交直线l于点D,过点C画CE⊥OC交直线l于点E.
(1)求∠OBA的度数,并直接写出直线AB的解析式;
(2)若点C的横坐标为2,求BE的长;
(3)当BE=1时,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
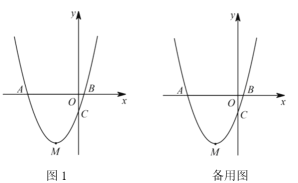
【题目】若关于![]() 的二次函数
的二次函数![]() (
(![]() 为常数)与
为常数)与![]() 轴交于两个不同的点
轴交于两个不同的点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其图象的顶点为点
,其图象的顶点为点![]() 是坐标原点.
是坐标原点.
(1)若![]() 、
、![]() 、
、![]() ,求此二次函数的解析式并写出二次函数的对称轴;
,求此二次函数的解析式并写出二次函数的对称轴;
(2)如图1,若![]() ,
,![]() ,
,![]() 为直角三角形,
为直角三角形,![]() 是以
是以![]() 的等边三角形,试确定
的等边三角形,试确定![]() 的值;
的值;
(3)设![]() 为正整数,且
为正整数,且![]() ,
,![]() ,
,![]() 为任意常数,令
为任意常数,令![]() ,
,![]() ,如果对于一切实数
,如果对于一切实数![]() ,
,![]() 始终成立,求
始终成立,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
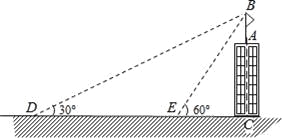
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.
查看答案和解析>>
科目:初中数学 来源: 题型:
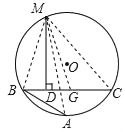
【题目】请阅读下列材料,并完成相应的任务:
阿基米德是有史以来最伟大的数学家之一,阿基米德的折弦定理是其推导出来的重要定理之一.阿基米德折弦定理:如图,AB和BC是⊙O的两条弦(即折线ABC是⊙O的一条折弦),BC>AB,M是弧ABC的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
证明:如图,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是弧ABC的中点,
∴MA=MC.
…
请按照上面的证明思路,写出该证明的剩余部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某甜品店计划订购一种鲜奶,根据以往的销售经验,当天的需求量与当天的最高气温T有关,现将去年六月份(按30天计算)的有关情况统计如下:(最高气温与需求量统计表)
最高气温(单位:摄氏度) | 需求量(单位:杯) |
T<25 | 250 |
| 300 |
| 400 |
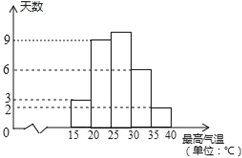
(1)求去年六月份最高气温不高于30℃的天数.
(2)若以最高气温位于各区间的频率估计最高气温位于该区间的概率,求去年六月份这种鲜奶一天的需求量不超过250杯的概率.
(3)若今年六月份每天的进货量均为350杯,每杯的进价为5元,售价为10元,未售出的这种鲜奶厂家以1元的价格收回销毁,假设今年与去年的情况大致一样,若今年六月份某天的最高气温T满足大于等于25℃小于30℃ ,试估计这一天销售这种鲜奶所获得的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com