
【题目】如图,在ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )
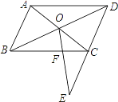
A. 1 B. 1.5 C. 2 D. 3
科目:初中数学 来源: 题型:
【题目】(8分)如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.
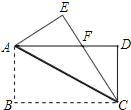
(1)试说明:AF=FC;
(2)如果AB=3,BC=4,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于![]() 的二次函数
的二次函数![]() (
(![]() 为常数)与
为常数)与![]() 轴交于两个不同的点
轴交于两个不同的点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其图象的顶点为点
,其图象的顶点为点![]() 是坐标原点.
是坐标原点.
(1)若![]() 、
、![]() 、
、![]() ,求此二次函数的解析式并写出二次函数的对称轴;
,求此二次函数的解析式并写出二次函数的对称轴;
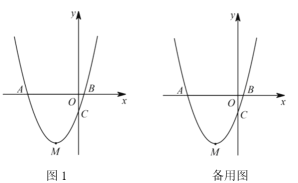
(2)如图1,若![]() ,
,![]() ,
,![]() 为直角三角形,
为直角三角形,![]() 是以
是以![]() 的等边三角形,试确定
的等边三角形,试确定![]() 的值;
的值;
(3)设![]() 为正整数,且
为正整数,且![]() ,
,![]() ,
,![]() 为任意常数,令
为任意常数,令![]() ,
,![]() ,如果对于一切实数
,如果对于一切实数![]() ,
,![]() 始终成立,求
始终成立,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务:
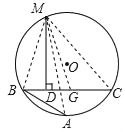
阿基米德是有史以来最伟大的数学家之一,阿基米德的折弦定理是其推导出来的重要定理之一.阿基米德折弦定理:如图,AB和BC是⊙O的两条弦(即折线ABC是⊙O的一条折弦),BC>AB,M是弧ABC的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
证明:如图,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是弧ABC的中点,
∴MA=MC.
…
请按照上面的证明思路,写出该证明的剩余部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:等腰Rt△ABC中,∠BAC=90°,BC=2,E为边AB上任意一点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠AED;②△AED∽△ECB;③AD∥BC;④四边形ABCD的面积有最大值,且最大值为![]() .其中正确的结论有_____.(填写所有正确结论的序号)
.其中正确的结论有_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某甜品店计划订购一种鲜奶,根据以往的销售经验,当天的需求量与当天的最高气温T有关,现将去年六月份(按30天计算)的有关情况统计如下:(最高气温与需求量统计表)
最高气温(单位:摄氏度) | 需求量(单位:杯) |
T<25 | 250 |
| 300 |
| 400 |
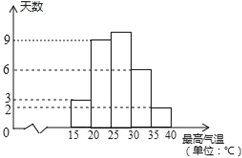
(1)求去年六月份最高气温不高于30℃的天数.
(2)若以最高气温位于各区间的频率估计最高气温位于该区间的概率,求去年六月份这种鲜奶一天的需求量不超过250杯的概率.
(3)若今年六月份每天的进货量均为350杯,每杯的进价为5元,售价为10元,未售出的这种鲜奶厂家以1元的价格收回销毁,假设今年与去年的情况大致一样,若今年六月份某天的最高气温T满足大于等于25℃小于30℃ ,试估计这一天销售这种鲜奶所获得的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
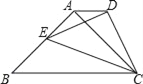
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com