
【题目】如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象交于A(一1,6)、B(a,一2)两点.
的图象交于A(一1,6)、B(a,一2)两点.
(1)求一次函数的解析式;
(2)连接OA、0B,求ΔAOB的面积;
(3)当x满足_______________时, 0<y1≤y2.
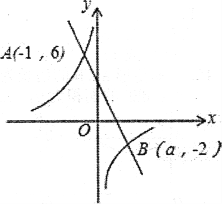
【答案】(1)![]() ;(2)8;(3)
;(2)8;(3)![]()
【解析】试题分析:(1)将点A的坐标代入y2=![]() 中,得到k2的值,将点B的坐标代入y2=
中,得到k2的值,将点B的坐标代入y2=![]() 中,得到a的值,再将A、B的值代入y1=k1x+b中,得到二元一次方程组,解方程组即可得出一次函数的解析式;(2)连接OA、OB,求y1与y轴交点坐标后,根据S△AOB=S△AOC+S△BOC求S△AOB的值;(3)写出y1图象在 y2图象下方时,对就x的取值范围即可;
中,得到a的值,再将A、B的值代入y1=k1x+b中,得到二元一次方程组,解方程组即可得出一次函数的解析式;(2)连接OA、OB,求y1与y轴交点坐标后,根据S△AOB=S△AOC+S△BOC求S△AOB的值;(3)写出y1图象在 y2图象下方时,对就x的取值范围即可;
试题解析:
解:∵A(一1,6)在反比例函数y2=![]() 的图象上,
的图象上,
∴k2=-6,
∴y2=![]() ,
,
∵点B(a,一2)在y2=![]() 图象上,
图象上,
∴a=3,
∴点B的坐标为(3,-2),
∵点A、B在一次函数y1=k1x+b的图象,
∴![]() 解得
解得![]()
∴一次函数的解析式为:y1=-2x+4;
(2)连接OA、OB,直线y1=-2x+4与y轴相交于点C(0,4),如图所示:
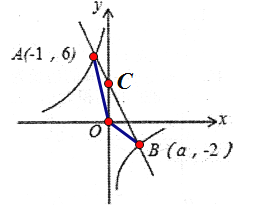
∵S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,S△AOB=S△AOC+S△BOC,
,S△AOB=S△AOC+S△BOC,
∴S△AOB=2+6=8;
(3)∵0<y1≤y2,由图象可得当![]() 时,y1的图象在y2的下方,
时,y1的图象在y2的下方,
∴![]() 。
。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( ) ①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为 ![]() ;
;
②直角三角形的最大边长为 ![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为 ![]() ;
;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结沦中,错误的有( ) ①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c , 若a2+b2=c2 , 则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy .
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
A. 16 B. 12 C. 24 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为 A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3) 
(1)求Rt△ABC的面积;
(2)在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com