
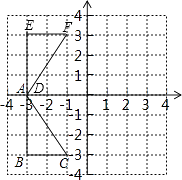
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为 A(﹣3,0),B(﹣3,﹣3),C(﹣1,﹣3) 
(1)求Rt△ABC的面积;
(2)在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F的坐标.
【答案】
(1)解:S△ABC= ![]() AB×BC=
AB×BC= ![]() ×3×2=3
×3×2=3
(2)解:所画图形如下所示,其中△DEF即为所求,
D,E,F的坐标分别为:D(﹣3,0),E(﹣3,3),F(﹣1,3).
【解析】(1)直接根据三角形的面积公式求解即可;(2)先找出△ABC各顶点关于x轴对称的对应点,然后顺次连接各点即可.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对坐标与图形变化-对称的理解,了解关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y).


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象交于A(一1,6)、B(a,一2)两点.
的图象交于A(一1,6)、B(a,一2)两点.
(1)求一次函数的解析式;
(2)连接OA、0B,求ΔAOB的面积;
(3)当x满足_______________时, 0<y1≤y2.
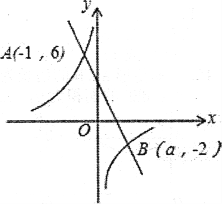
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.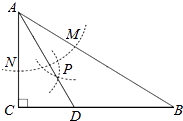
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE⊥AB于E,若DE=1cm,∠CBD=30°,求∠A的度数和AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象经过点(1,2),点(﹣1,6),且与x轴交于点B,与y轴交于点A. 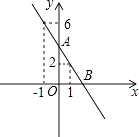
(1)求出这个一次函数的解析式;
(2)求出一次函数图象与两坐标轴围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
A.本次抽查活动共抽查了2100名学生
B.本次抽查活动中视力不低于4.8的学生人数占总人数的66.7%
C.本次抽查活动中视力不低于4.8学生人数中的极差为300人
D.由活动结果可以知道随着年级的增长,视力低于4.8的人数越来越多,呈上升趋势,那么同年级中抽到视力不低于4.8的学生的概率将越来越小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com