
【题目】在![]() 中,
中,![]() ,点
,点![]() 与点
与点![]() 在
在![]() 同侧,
同侧,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)如图1,当![]() 时,线段
时,线段![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
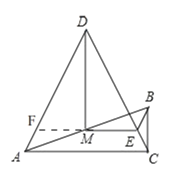
(2)如图2,当![]() 时,试探究线段
时,试探究线段![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
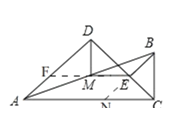
(3)如图3,当![]() 时,求
时,求![]() 的值.
的值.
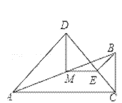
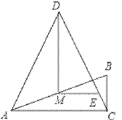
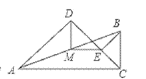
图1 图2 图3
【答案】(1) ![]() ;(2)见解析:(3)
;(2)见解析:(3)![]() .
.
【解析】
(1)首先延长![]() 交
交![]() 于
于![]() ,由BE∥DA,得出∠FAM=∠EBM,AM=BM,∠AMF=∠BME,得出△AMF≌△BME,进而得出AF=BE,MF=ME,又由DA=DC,∠ADC=90°,得出∠BED=∠ADC=90°,∠ACD=45°,再根据∠ACB=90°,得出∠ECB=∠EBC=45°,得出CE=BE=AF,DF=DE,得出DM⊥EF,DM平分∠ADC,∠MDE=45°,即可得出MD=ME.
,由BE∥DA,得出∠FAM=∠EBM,AM=BM,∠AMF=∠BME,得出△AMF≌△BME,进而得出AF=BE,MF=ME,又由DA=DC,∠ADC=90°,得出∠BED=∠ADC=90°,∠ACD=45°,再根据∠ACB=90°,得出∠ECB=∠EBC=45°,得出CE=BE=AF,DF=DE,得出DM⊥EF,DM平分∠ADC,∠MDE=45°,即可得出MD=ME.
(2)首先延长![]() 交
交![]() 于
于![]() ,由BE∥DA,得出∠FAM=∠EBM,AM=BM,∠AMF=∠BME,得出△AMF≌△BME,进而得出AF=BE,MF=ME,又由DA=DC,∠ADC=60°,得出∠BED=∠ADC=60°,∠ACD=60°,再根据∠ACB=90°,得出∠ECB=∠EBC=30°,得出CE=BE=AF,DF=DE,得出DM⊥EF,DM平分∠ADC,∠MDE=30°,在Rt△MDE中,即可得出
,由BE∥DA,得出∠FAM=∠EBM,AM=BM,∠AMF=∠BME,得出△AMF≌△BME,进而得出AF=BE,MF=ME,又由DA=DC,∠ADC=60°,得出∠BED=∠ADC=60°,∠ACD=60°,再根据∠ACB=90°,得出∠ECB=∠EBC=30°,得出CE=BE=AF,DF=DE,得出DM⊥EF,DM平分∠ADC,∠MDE=30°,在Rt△MDE中,即可得出![]()
(3)首先延长![]() 交
交![]() 于
于![]() ,由BE∥DA,得出∠FAM=∠EBM,AM=BM,∠AMF=∠BME,得出△AMF≌△BME,进而得出AF=BE,MF=ME,再延长
,由BE∥DA,得出∠FAM=∠EBM,AM=BM,∠AMF=∠BME,得出△AMF≌△BME,进而得出AF=BE,MF=ME,再延长![]() 交
交![]() 于点N,得出∠BNC=∠DAC,又由DA=DC,得出∠DCA=∠DAC=∠BNC,∠ACB=90°,得出∠ECB=∠EBC,CE=BE=AF,DF=DE,从而得出DM⊥EF,DM平分∠ADC,在Rt△MDE中,即可得出
于点N,得出∠BNC=∠DAC,又由DA=DC,得出∠DCA=∠DAC=∠BNC,∠ACB=90°,得出∠ECB=∠EBC,CE=BE=AF,DF=DE,从而得出DM⊥EF,DM平分∠ADC,在Rt△MDE中,即可得出![]() 的值.
的值.
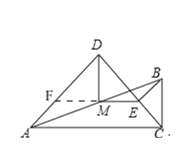
(1)![]() .如图,延长
.如图,延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
故答案为:![]() ;
;
(2)![]() ,理由:
,理由:
如图,延长![]() 交
交![]() 于
于![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.
(3)如图,延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
延长![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
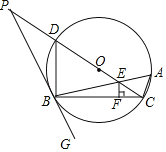
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=-x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点
交于点A(1,m),这两条直线分别与x轴交于B,C两点
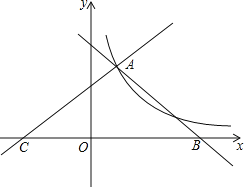
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中![]() 条直线为
条直线为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,点
,点![]() 关于
关于![]() 轴对称,抛物线
轴对称,抛物线![]() 过
过![]() 三点,下列判断中:①
三点,下列判断中:①![]() ;②
;②![]() ;③抛物线关于直线
;③抛物线关于直线![]() 对称;④抛物线过点
对称;④抛物线过点![]() ;⑤四边形
;⑤四边形![]() ,其中正确的个数有( )
,其中正确的个数有( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果记y=![]() =f(x),并且f(1)表示当x=1时y的值.即f(1)=
=f(x),并且f(1)表示当x=1时y的值.即f(1)=![]() =
=![]() ;f(
;f(![]() )表示当x=
)表示当x=![]() 时y的值,f(
时y的值,f(![]() )=
)=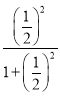 =
=![]() …,那么f(﹣1)+f(﹣2)+f(﹣
…,那么f(﹣1)+f(﹣2)+f(﹣![]() )+f(﹣3)+f(﹣
)+f(﹣3)+f(﹣![]() )+…+f(﹣2019)+f(﹣
)+…+f(﹣2019)+f(﹣![]() )=_____.
)=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形ABOC的边OB在x轴上,过点C(3,4)的双曲线与AB交于点D,且AC=2AD,则点D的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
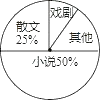
【题目】九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)九年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出 2 名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的 2 人恰好是乙和丙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com