
【题目】在直角坐标系中,已知A(0,1),B(10,1),C(9,4).

(1)在网格中画出过A、B、C三点的圆和直线![]() 的图像;
的图像;
(2)已知P是直线![]() 上的点,且△APB是直角三角形,那么符合条件的点P共有 个;
上的点,且△APB是直角三角形,那么符合条件的点P共有 个;
(3)如果直线![]() (k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ,则k= .
(k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ,则k= .
【答案】(1)见解析;(2)4;(3)![]()
【解析】
(1)首先连接AB、BC,分别作出它们的垂直平分线交于一点M,以M点为圆心,MA长为半径作圆即可;在直角坐标系中,先描点,再连线即可作出直线![]() 的图象;
的图象;
(2)分A为直角顶点、B为直角顶点、P为直角顶点三种情况讨论,依此即可得到符合条件的点P的个数;
(3)直线y=kx(k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ,而直线y=kx(k>0)是正比例函数,一定经过原点,故不可能经过点A,则直线y=kx(k>0)过点B,用待定系数法求出的k值即可.
(1)作图如下:⊙M和直线![]() 即为所求;
即为所求;
(2)如图所示:
当A为直角顶点时,过A点作AP⊥AB交直线![]() 于P点,
于P点,

B为直角顶点时,过B点作BP⊥AB交直线![]() 于P点,
于P点,
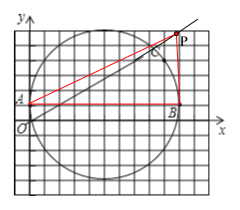
P为直角顶点时,P点为以AB为直径的圆与直线![]() 的交点,
的交点,
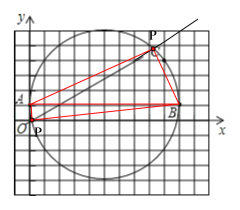
故P是直线![]() 上的点,且△APB是直角三角形,那么符合条件的点P共有4个.
上的点,且△APB是直角三角形,那么符合条件的点P共有4个.
故答案为:4;
(3)直线y=kx(k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ,而直线y=kx(k>0)是正比例函数,一定经过原点,故不可能经过点A,则直线y=kx(k>0)过点B,把B(10,1)代入得:
10k=1
∴k=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC各边为边分别向外作等边三角形,编号为①、②、③,将②、①如图所示依次叠在③上,已知四边形EMNC与四边形MPQN的面积分别为9![]() 与7
与7![]() ,则斜边BC的长为( )
,则斜边BC的长为( )
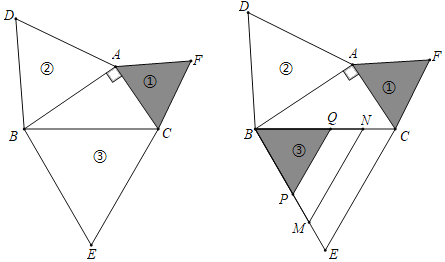
A.5B.9C.10D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是决胜全面建成小康社会冲锋之年,为进一步加快脱贫攻坚步伐,某市出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
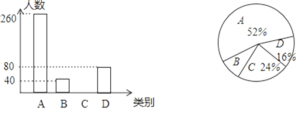
请根据图中信息回答下面的问题:
(1)求本次抽样调查贫困户总户数,并补全条形统计图;
(2)若该地共有15000户贫困户,请估计至少得到3项帮扶措施的大约有多少户;
(3)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用列表法或画树状图的方法,求出恰好选中甲和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
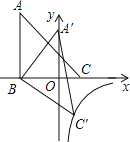
【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=![]() 的图象上,则k的值为__.
的图象上,则k的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
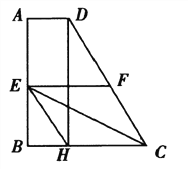
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
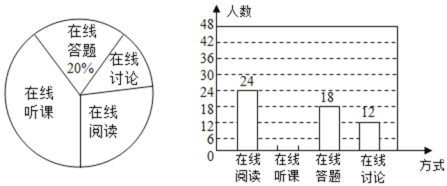
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com