
【题目】如图,以Rt△ABC各边为边分别向外作等边三角形,编号为①、②、③,将②、①如图所示依次叠在③上,已知四边形EMNC与四边形MPQN的面积分别为9![]() 与7
与7![]() ,则斜边BC的长为( )
,则斜边BC的长为( )
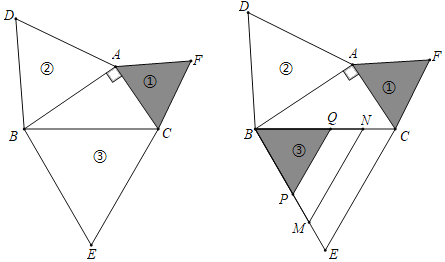
A.5B.9C.10D.16
【答案】C
【解析】
设等边三角形△EBC,△ABD,△ACF的面积分别是S3,S2,S1,AC=b,BC=a,AB=c,根据勾股定理得到c2+b2=a2,根据等式的性质得到![]() c2+
c2+![]() b2=
b2=![]() a2.根据等边三角形的面积公式得到S3=
a2.根据等边三角形的面积公式得到S3=![]() a2,S2=
a2,S2=![]() c2,S1=
c2,S1=![]() b2,根据已知条件列方程即可得到结论.
b2,根据已知条件列方程即可得到结论.
解:如图,设等边三角形△EBC,△ABD,△ACF的面积分别是S3,S2,S1,AC=b,BC=a,AB=c,
∵△ABC是直角三角形,且∠BAC=90度,
∴c2+b2=a2,
∴![]() c2+
c2+![]() b2=
b2=![]() a2.
a2.
∵S3=![]() a2,S2=
a2,S2=![]() c2,S1=
c2,S1=![]() b2,
b2,
∴S3﹣S2=![]() (a2﹣c2)=
(a2﹣c2)=![]() b2=9
b2=9![]() ,S3﹣S1=
,S3﹣S1=![]() a2﹣
a2﹣![]() b2=
b2=![]() (a2﹣b2)=
(a2﹣b2)=![]() c2=
c2=![]() +
+![]() =
=![]() ,
,
∴b=6,c=8,
即AB=8,AC=6,
∴BC=![]() =
=![]() =10,
=10,
故选:C.


科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)![]() =1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:
=1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:![]() °≈0.73,cos8°≈0.67,tan48°≈1.11)
°≈0.73,cos8°≈0.67,tan48°≈1.11)
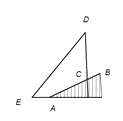
A.17.0米B.21.9米C.23.3米D.33.3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:对任意一个n位正整数M(n≥3),若M与它的十位数字的p倍的差能被整数q整除,则称这个数为“p阶q级数”,例如:712是“5阶7级数”,因为![]() =101;712也是“12阶10级数”,因为
=101;712也是“12阶10级数”,因为![]() =70.
=70.
(1)若415是“5阶k级数”,且k<300,求k的最大值;
(2)若一个四位数M的百位数字比个位数字大2,十位数字为1,且M既是“4阶13级数”又是“6阶5级数”,求这个四位数M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D.
(1)求证:直线AC是⊙O的切线;
(2)若∠A=30°,⊙O的半径是2,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校八年级学生数学学习情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为4个等级:A、B、C、D,并将统计结果绘制成两幅不完整的统计图,请根据图中的信息解答下列问题
(1)补全条形统计图
(2)等级为D等的所在扇形的圆心角是 度
(3)如果八年级共有学生1800名,请你估算我校学生中数学学习A等和B等共多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年伊始,一场突如其来的疫情防控战在中华大地骤然打响,全国人民自觉居家减少外出,师生停课不停学,举国共抗疫情.某中学在复学后,为了了解学生们在居家期间的生活状态,以更好地保护复学后学生们的身心健康,对本校学生进行了“居家期间学习之余主要活动”的抽样调查.种类为:(A)强身健体、(B)艺术熏陶、(C)经典阅读、(D)分担劳动、(E)其他.针对以上活动种类,统计学生们花时间最多的种类的人数,以绘制成如下两幅不完整的条形统计图和扇形统计图.
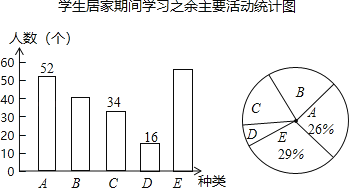
请根据图中的信息,回答下列问题.
(1)被抽样调查的总人数为 人;
(2)补全条形统计图;
(3)若该校共有学生1800人,请估算种类D的大约人数;
(4)据此疫情经历,给自己提出一条人生建议 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,作∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,连接EF.若AE=16,AF=10,则BF的长为( ).
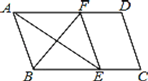
A.10B.12C.14D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知A(0,1),B(10,1),C(9,4).

(1)在网格中画出过A、B、C三点的圆和直线![]() 的图像;
的图像;
(2)已知P是直线![]() 上的点,且△APB是直角三角形,那么符合条件的点P共有 个;
上的点,且△APB是直角三角形,那么符合条件的点P共有 个;
(3)如果直线![]() (k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ,则k= .
(k>0)上有且只有二个点Q与点A、点B两点构成直角△ABQ,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为边AD上一点(不为端点),EF⊥AD交AC于点F,要求△FBC的面积,只需知道下列哪个三角形的面积即可( )
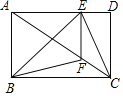
A.△EBCB.△EBFC.△ECDD.△EFC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com