
【题目】2020年伊始,一场突如其来的疫情防控战在中华大地骤然打响,全国人民自觉居家减少外出,师生停课不停学,举国共抗疫情.某中学在复学后,为了了解学生们在居家期间的生活状态,以更好地保护复学后学生们的身心健康,对本校学生进行了“居家期间学习之余主要活动”的抽样调查.种类为:(A)强身健体、(B)艺术熏陶、(C)经典阅读、(D)分担劳动、(E)其他.针对以上活动种类,统计学生们花时间最多的种类的人数,以绘制成如下两幅不完整的条形统计图和扇形统计图.
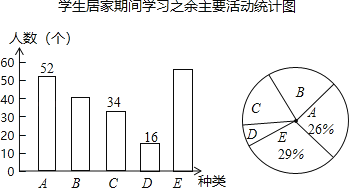
请根据图中的信息,回答下列问题.
(1)被抽样调查的总人数为 人;
(2)补全条形统计图;
(3)若该校共有学生1800人,请估算种类D的大约人数;
(4)据此疫情经历,给自己提出一条人生建议 .
【答案】(1)200人;(2)画图见解析;(3)144人;(4)响应国家号召,停课不停学,在完成学业的前提下,强身健体,加强身体的免疫力.
【解析】
(1)根据选择A的人数和所占的百分比,可以求得本次调查的总人数;
(2)根据(1)中的结果可以得到选择B的人数,从而可以将条形统计图补充完整,然后根据条形统计图中的数据可以计算出扇形统计图中E所对应的圆心角的度数;
(3)根据统计图中的数据可以计算出该校学生选择C有多少人;
(4)提出一条合理的人生建议即可.
解:(1)这次调查的总人数是:52÷26%=200(人),
故答案为:200;
(2)选择E的学生有200×29%=58(人),选择B的学生有:200﹣52﹣34﹣16﹣58=40(人),
补全的条形统计图如右图所示,
(3)1800×![]() =144(人),
=144(人),
答:选择D有144人;
(4)响应国家号召,停课不停学,在完成学业的前提下,强身健体,加强身体的免疫力.
故答案为:响应国家号召,停课不停学,在完成学业的前提下,强身健体,加强身体的免疫力.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.

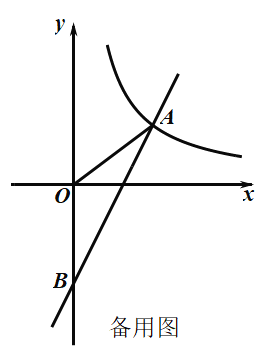
(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
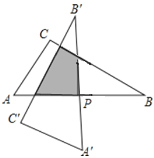
【题目】如图,在![]() 中,已知:
中,已知:![]() ,
,![]() ,
,![]() ,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转
,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转前后两个直角三角形重叠部分的面积为__________
,则旋转前后两个直角三角形重叠部分的面积为__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的等边△ABC中,AD是BC边上的中线,点E是△ABC内一个动点,且DE=2,将线段AE绕点A逆时针旋转60°得到AF,则DF的最小值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC各边为边分别向外作等边三角形,编号为①、②、③,将②、①如图所示依次叠在③上,已知四边形EMNC与四边形MPQN的面积分别为9![]() 与7
与7![]() ,则斜边BC的长为( )
,则斜边BC的长为( )
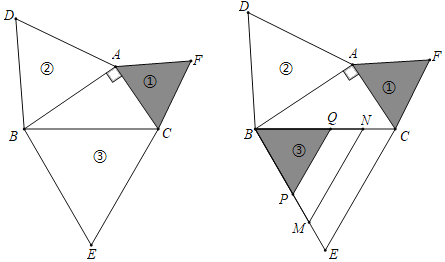
A.5B.9C.10D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
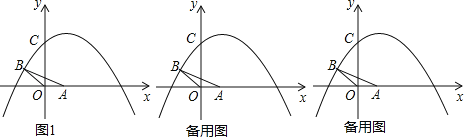
【题目】如图1,平面直角坐标系中,△OAB的边OA在x轴的正半轴上,点B在第二象限,且∠AOB=135°,OA=2,OB=2![]() ,抛物线y=﹣
,抛物线y=﹣![]() x2+bx+c经过点B,并与y轴交于点C(0,5),点P在抛物线的对称轴上.
x2+bx+c经过点B,并与y轴交于点C(0,5),点P在抛物线的对称轴上.
(1)求b、c的值,及抛物线的对称轴.
(2)求证:以点M(2,5)为圆心,半径为2![]() 的圆与边AB相切.
的圆与边AB相切.
(3)若满足条件∠AOB+∠POD=180°与OB:OD=OA:OP的点D恰好在抛物线上,请求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是决胜全面建成小康社会冲锋之年,为进一步加快脱贫攻坚步伐,某市出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
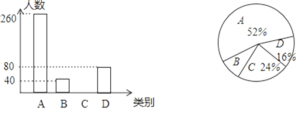
请根据图中信息回答下面的问题:
(1)求本次抽样调查贫困户总户数,并补全条形统计图;
(2)若该地共有15000户贫困户,请估计至少得到3项帮扶措施的大约有多少户;
(3)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用列表法或画树状图的方法,求出恰好选中甲和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
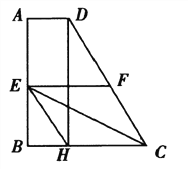
查看答案和解析>>
科目:初中数学 来源: 题型:
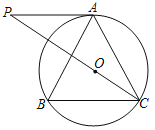
【题目】如图,△ABC内接于⊙O,AB=AC,过A作AP∥BC交CO的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若BC=8,tanB=2,求PA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com