
【题目】如图,在![]() 中,已知:
中,已知:![]() ,
,![]() ,
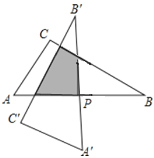
,![]() ,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转
,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转前后两个直角三角形重叠部分的面积为__________
,则旋转前后两个直角三角形重叠部分的面积为__________![]() .
.
【答案】![]()
【解析】
如图,在Rt△DPB中, 根据勾股定理求得DP=![]() ,再证明△B′PH≌△BPD,根据全等三角形的性质可得PH=PD=
,再证明△B′PH≌△BPD,根据全等三角形的性质可得PH=PD=![]() ;在直角△BGH中,BH=3+
;在直角△BGH中,BH=3+![]() ,可求得GH=
,可求得GH=![]() ,BG=
,BG=![]() (3+
(3+![]() ),根据SDGHP= S△BGH- S△BDP即可求得重合部分的面积.
),根据SDGHP= S△BGH- S△BDP即可求得重合部分的面积.
如图,在直角△DPB中,BP=AP=AC=3,设DP=x,
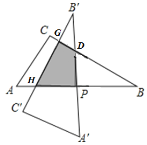
∵∠A=60°,
∴DP2+BP2=BD2,
∴x2+32=(2x)2,
∴DP=x=![]() ,
,
∵在△B′PH和△BPD中,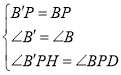 ,
,
∴△B′PH≌△BPD,
∴PH=PD=![]() ,
,
∵在直角△BGH中,BH=3+![]() ,
,
∴GH=![]() ,BG=
,BG=![]() (3+
(3+![]() ),
),
∴S△BGH=![]() ×
×![]() ×
×![]() (3+
(3+![]() )=
)=![]() ,S△BDP=
,S△BDP=![]() ×3×
×3×![]() =
=![]() ,
,
∴SDGHP=![]() -
-![]() =
=![]() cm2.
cm2.
故答案为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有独立包装的口罩,其中粉色口罩有3个、蓝色口罩有2个,这些口罩除了颜色外全部相同,从中随机依次不放回拿出两个口罩,则两个口罩都是粉色的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为普及防治新型冠状病毒感染的科学知识和有效方法,不断增强同学们的自我保护意识,学校举办了新型冠状病毒疫情防控网络知识竞答活动,试卷题目共10题,每题10分.现分别从七年级的三个班中各随机取10名同学的成绩(单位:分),收集数据如表:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 | a | 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | |
2班 | 83 | c | d |
3班 | b | 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让同学们重视疫情防控知识的学习,学校将给竞答成绩满分的同学颁发奖状,该校七年级新生共600人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,0,1,![]() ,
,![]() ,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣
,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣![]() =
=![]() 的解为正数的a共有( )
的解为正数的a共有( )
A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:对任意一个n位正整数M(n≥3),若M与它的十位数字的p倍的差能被整数q整除,则称这个数为“p阶q级数”,例如:712是“5阶7级数”,因为![]() =101;712也是“12阶10级数”,因为
=101;712也是“12阶10级数”,因为![]() =70.
=70.
(1)若415是“5阶k级数”,且k<300,求k的最大值;
(2)若一个四位数M的百位数字比个位数字大2,十位数字为1,且M既是“4阶13级数”又是“6阶5级数”,求这个四位数M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
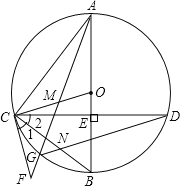
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BD平分∠ABC,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好经过点D.
(1)求证:直线AC是⊙O的切线;
(2)若∠A=30°,⊙O的半径是2,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年伊始,一场突如其来的疫情防控战在中华大地骤然打响,全国人民自觉居家减少外出,师生停课不停学,举国共抗疫情.某中学在复学后,为了了解学生们在居家期间的生活状态,以更好地保护复学后学生们的身心健康,对本校学生进行了“居家期间学习之余主要活动”的抽样调查.种类为:(A)强身健体、(B)艺术熏陶、(C)经典阅读、(D)分担劳动、(E)其他.针对以上活动种类,统计学生们花时间最多的种类的人数,以绘制成如下两幅不完整的条形统计图和扇形统计图.
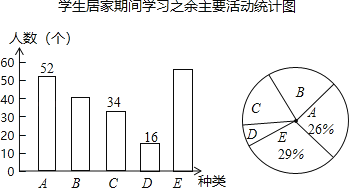
请根据图中的信息,回答下列问题.
(1)被抽样调查的总人数为 人;
(2)补全条形统计图;
(3)若该校共有学生1800人,请估算种类D的大约人数;
(4)据此疫情经历,给自己提出一条人生建议 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6,点D为AC中点,点E为边AB上一动点,点F为射线BC上一动点,且∠FDE=90°.
(1)当DF∥AB时,连接EF,求∠DEF的余切值;
(2)当点F在线段BC上时,设AE=x,BF=y,求y关于x的函数关系式,并写出x的取值范围;
(3)连接CE,若△CDE为等腰三角形,求BF的长.
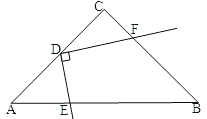
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com