
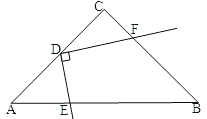
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6,点D为AC中点,点E为边AB上一动点,点F为射线BC上一动点,且∠FDE=90°.
(1)当DF∥AB时,连接EF,求∠DEF的余切值;
(2)当点F在线段BC上时,设AE=x,BF=y,求y关于x的函数关系式,并写出x的取值范围;
(3)连接CE,若△CDE为等腰三角形,求BF的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)6或7
;(3)6或7
【解析】
(1)先根据勾股定理求出AB的长,再由三角形的中位线定理求出DF的长,利用等腰直角三角形的性质求出DE的长,由锐角三角函数的定义即可求出∠DEF的余切值;
(2)过点E作EH⊥AC于点H,由平行线的性质及等腰三角形的性质可求出HE、HD的表达式,再由相似三角形的判定定理求出△HDE∽△CFD,根据相似三角形的性质可写出y关于x的函数关系式;
(3)先分析出△DCE为等腰三角形时的两种情况,再根据题意画出图形,当DC=DE时,证明∠AEC=90°,得到AE=CE,再根据等腰三角形三线合一得到DE⊥AC,从而得到F与C重合,进而得出BF的长;当ED=EC时,先判断出点F的位置,再根据相似三角形的性质及判定定理即可解答.
(1)∵AC=BC=6,∠ACB=90°,
∴∠A=∠B=45°,![]() .
.
∵DF∥AB,![]() ,
,
∴∠AED=∠EDF=90°,![]() ,
,
∴△ADE是等腰直角三角形,
∴![]() .
.
在Rt△DEF中,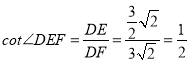 ;
;
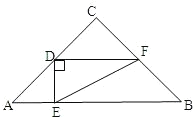
(2)过点E作EH⊥AC于点H.
∵BC⊥AC,
∴EH∥BC,
∴∠AEH=∠B.
∵∠B=∠A,
∴∠AEH=∠A,![]() ,
,
∴![]() .
.
∵∠EDF=90°,
∴∠EDH+∠CDF=90°.
∵∠C=90°,
∴∠CDF+∠CFD=90°,
∴∠EDH=∠CFD.
∵∠EHD=∠C=90°,
∴△HDE∽△CFD,
∴![]() ,
,
∴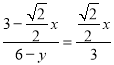 ,
,
∴![]() ;
;
(3)∵![]() ,CD=3,
,CD=3,
∴CE>CD,
∴若△DCE为等腰三角形,只有DC=DE或ED=EC两种可能.
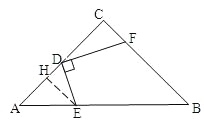
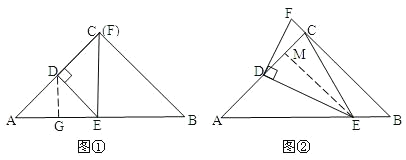
①当DC=DE时,(如图①)
∵DC=DE,
∴∠DCE=∠DEC.
∵AD=CD,DE=DC,
∴AD=DE,
∴∠A=∠AED.
∵∠A+∠AED+∠DEC+∠DCE=180°,
∴∠AED+∠DEC=90°,
∴∠AEC=90°,
∴CE⊥AB.
∵AC=BC,
∴AE=![]() AB=
AB=![]() ,
,
∵∠A=45°,∠AEC=90°,
∴AE=CE.
∵AD=CD,
∴DE⊥AC,
∴此时F与C重合,
∴BF=6;
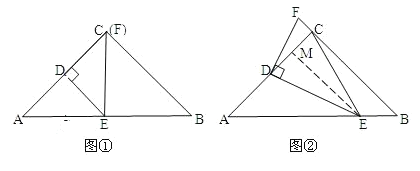
②当ED=EC时,点F在BC的延长线上,
过点E作EM⊥CD于点M,(如图②)
∵ED=EC,EM⊥CD,
∴DM=![]() CD=
CD=![]() .
.
∵EM⊥CD,
∴△DME是直角三角形.
∵DE⊥DF,
∴∠EDM+∠FDC=90°.
∵∠FDC+∠F=90°,
∴∠F=∠EDM,
∴△DFC∽△EDM,
∴![]() ,
,
∴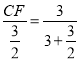 ,
,
∴CF=1,
∴BF=7,
综上所述:BF为6或7.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
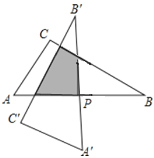
【题目】如图,在![]() 中,已知:
中,已知:![]() ,
,![]() ,
,![]() ,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转
,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转前后两个直角三角形重叠部分的面积为__________
,则旋转前后两个直角三角形重叠部分的面积为__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是决胜全面建成小康社会冲锋之年,为进一步加快脱贫攻坚步伐,某市出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
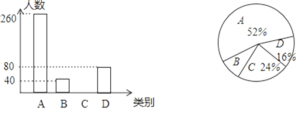
请根据图中信息回答下面的问题:
(1)求本次抽样调查贫困户总户数,并补全条形统计图;
(2)若该地共有15000户贫困户,请估计至少得到3项帮扶措施的大约有多少户;
(3)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用列表法或画树状图的方法,求出恰好选中甲和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
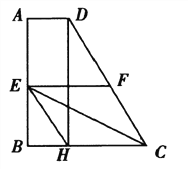
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
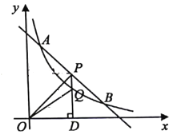
(1)求反比例函数和一次函数的解析式;
(2)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
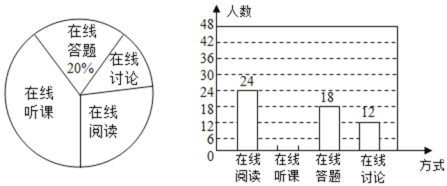
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
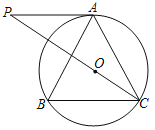
【题目】如图,△ABC内接于⊙O,AB=AC,过A作AP∥BC交CO的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若BC=8,tanB=2,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=2,AB=3,BC=4,点G是△ABC的重心.将△ABC平移,使得顶点A与点G重合.那么平移后的三角形与原三角形重叠部分的周长为( )
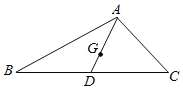
A.2B.3C.4D.4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com