
【题目】从﹣2,0,1,![]() ,
,![]() ,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣
,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣![]() =
=![]() 的解为正数的a共有( )
的解为正数的a共有( )
A.2个B.3个C.4个D.1个
【答案】A
【解析】
根据关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,可得抛物线对称轴小于﹣1,根据关于x的分式方程2﹣![]() =
=![]() 的解为正数,可得x>0,解得a>﹣3,进而可得a的取值范围,得结论.
的解为正数,可得x>0,解得a>﹣3,进而可得a的取值范围,得结论.
解:∵关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,
∴抛物线对称轴方程x=![]() ,
,
即![]() <﹣1,
<﹣1,
解得a<1,
∵关于x的分式方程2﹣![]() =
=![]() 的解为正数,
的解为正数,
∴x>0,
解分式方程,得x=2a+6,
∴2a+6>0,
解得a>﹣3,
∴﹣3<a<1,
∵从﹣2,0,1,![]() ,
,![]() ,3这六个数中,随机抽取一个数记为a,
,3这六个数中,随机抽取一个数记为a,
∴符合条件的正数a共有2个,为﹣2,0.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.
(1)求证:DH是⊙O的切线;
(2)若⊙O的半径为4,AE=FE时,求![]() 的长(结果保留π);
的长(结果保留π);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.

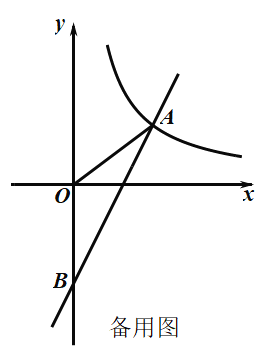
(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现
如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.

填空:
①∠DCE的度数是 ;
②线段CA、CE、CD之间的数量关系是 .
(2)探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)应用
如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情.为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传.某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析,过程如下:
(收集数据)
甲班15名学生测试成绩分别为:78,83,89,97,98,85,100,94,87,90,93,92,99,95;100.
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
(整理数据):
班级 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
甲 | 1 | 1 | 3 | 4 | 6 |
乙 | 1 | 2 | 3 | 5 | 4 |
(分析数据):
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 92 | a | 93 | 47.3 |
乙 | 90 | 87 | b | 50.2 |
(应用数据):
(1)根据以上信息,可以求出:a=_____分,b=______分;
(2)若规定测试成绩92分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
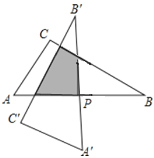
【题目】如图,在![]() 中,已知:
中,已知:![]() ,
,![]() ,
,![]() ,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转
,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转前后两个直角三角形重叠部分的面积为__________
,则旋转前后两个直角三角形重叠部分的面积为__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的等边△ABC中,AD是BC边上的中线,点E是△ABC内一个动点,且DE=2,将线段AE绕点A逆时针旋转60°得到AF,则DF的最小值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
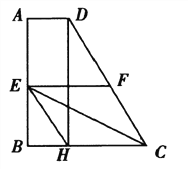
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com