
【题目】(1)发现
如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.

填空:
①∠DCE的度数是 ;
②线段CA、CE、CD之间的数量关系是 .
(2)探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)应用
如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.
【答案】(1)①120°,②CA=CE+CD;(2)∠DCE=90°;![]() CA=CD+CE.理由见解析;(3)DA=5
CA=CD+CE.理由见解析;(3)DA=5![]() 或
或![]() .
.
【解析】
(1)①证△BAD≌△CAE,从而得出∠ACE=∠B=60°,进而得出∠DCE的大小;
②根据△BAD≌△CAE可知BD=CE,从而得出CA=CE+CD;
(2)先证△BAD≌△CAE,得出BD=CE,然后在等腰直角三角形ABC中,得出CB=![]() CA,从而得出CA、CE、CD之间的数量关系;
CA,从而得出CA、CE、CD之间的数量关系;
(3)如下图,先证点B,C,A,D四点共圆,得出△ADE是等腰直角三角形,最后在Rt△BED中,利用勾股定理可求得.
(1)发现
解:①∵在△ABC中,AB=AC,∠BAC=60°,
∴∠BAC=∠DAE=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
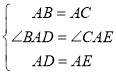 ,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,
∴∠DCE=∠ACE+∠ACB=60°+60°=120°;
故答案为:120°,
②∵△BAD≌△CAE,
∴BD=CE,
∴BC=BD+CD=EC+CD,
∴CA=BC=CE+CD;
故答案为:CA=CE+CD.
(2)探究
∠DCE=90°;![]() CA=CD+CE.
CA=CD+CE.
理由:∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE.
∴△BAD≌△CAE(SAS).
∴BD=CE,∠B=∠ACE=45°.
∴∠DCE=∠ACB+∠ACE=90°.
在等腰直角三角形ABC中,CB=![]() CA,
CA,
∵CB=CD+DB=CD+CE,
∴![]() CA=CD+CE.
CA=CD+CE.
(3)应用
DA=5![]() 或
或![]() .
.
作DE⊥AB于E,连接AD,
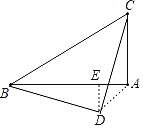
∵在Rt△ABC中,AB=6,AC=4,∠BAC=90°,
∴BC=![]() =
=![]() =2
=2![]() ,
,
∵∠BDC=90°,DB=DC,
∴DB=DC=![]() ,∠BCD=∠CBD=45°,
,∠BCD=∠CBD=45°,
∵∠BDC=∠BAC=90°,
∴点B,C,A,D四点共圆,
∴∠DAE=45°,
∴△ADE是等腰直角三角形,
∴AE=DE,
∴BE=6﹣DE,
∵BE2+DE2=BD2,
∴DE2+(6﹣DE)2=26,
∴DE=1,DE=5,
∴AD=![]() 或AD=5
或AD=5![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①为了了解一批灯泡的使用寿命,应采用全面调查的方式
②一组数据5,6,7,6, 8,10的众数和中位数都是6
③已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是m≥0
④式子![]() 有意义的条件是
有意义的条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
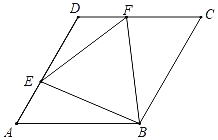
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《水浒传》《三国演义》《西游记》《红楼梦》(按照成书先后顺序)是中国古典长篇小说四大名著.
(1)小黄从这4部名著中,随机选择1部阅读,求他选中《西游记》的概率.
(2)某初中拟从这4部名著中,选择2部作为课外阅读书籍,求《西游记》被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为普及防治新型冠状病毒感染的科学知识和有效方法,不断增强同学们的自我保护意识,学校举办了新型冠状病毒疫情防控网络知识竞答活动,试卷题目共10题,每题10分.现分别从七年级的三个班中各随机取10名同学的成绩(单位:分),收集数据如表:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 | a | 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | |
2班 | 83 | c | d |
3班 | b | 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让同学们重视疫情防控知识的学习,学校将给竞答成绩满分的同学颁发奖状,该校七年级新生共600人,试估计需要准备多少张奖状?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,0,1,![]() ,
,![]() ,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣
,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣![]() =
=![]() 的解为正数的a共有( )
的解为正数的a共有( )
A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
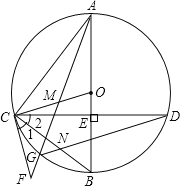
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称或中心对称变换,若原来点 A 坐标是(a,b),则经过第 2012 次变换后所得的 A 点坐标是( )
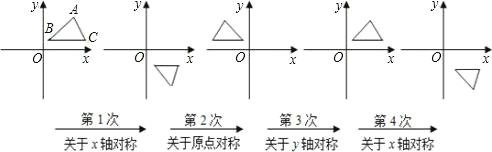
A. (a,b) B. (a,﹣b) C. (﹣a,b) D. (﹣a,﹣b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com