
【题目】《水浒传》《三国演义》《西游记》《红楼梦》(按照成书先后顺序)是中国古典长篇小说四大名著.
(1)小黄从这4部名著中,随机选择1部阅读,求他选中《西游记》的概率.
(2)某初中拟从这4部名著中,选择2部作为课外阅读书籍,求《西游记》被选中的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)有4本书就是4种情况,选择1本的概率即为![]() .
.
(2)把4本书编上号,把选出2本的所有可能结果写出来,再用选到《西游记》的情况的数量除以总结果数量就可以得出结果.
解:(1)小黄从这4部名著中,随机选择1部阅读,共有4种不同的选法,故选中《西游记》的概率为![]() .
.
(2)将4部名著《水浒传》《三国演义》《西游记》《红楼梦》分别记为A、B、C、D,设选择2部名著,其中《西游记》被选中的事件为M. 从4部名著中,任选2部的所有可能的结果为:(A,B) ; (A,C) ; (A,D) ; (B,C) ; (B,D) ; (C,D)共6种.
若其中必有《西游记》的有: (A,C);(B,C);(C,D) 3种,
![]() .
.


科目:初中数学 来源: 题型:
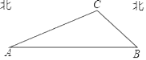
【题目】如图所示,要在某东西走向的A、B两地之间修一条笔直的公路,在公路起点A处测得某农户C在A的北偏东68°方向上.在公路终点B处测得该农户c在点B的北偏西45°方向上.已知A、B两地相距2400米.
(1)求农户c到公路B的距离;(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
(2)现在由于任务紧急,要使该修路工程比原计划提前4天完成,需将该工程原定的工作效率提高20%,求原计划该工程队毎天修路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1至图3中,![]() 的直径
的直径![]() ,
,![]() 切
切![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() .
.
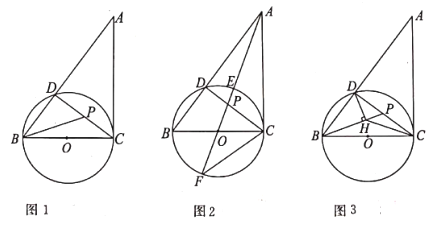
(1)如图1,当点![]() ,
,![]() 的距离最小时,求
的距离最小时,求![]() 的长;
的长;
(2)如图2,若射线![]() 过圆心
过圆心![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如图3,作![]() 于点
于点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
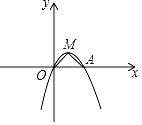
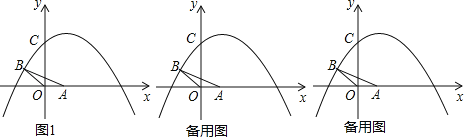
【题目】如图,在平面直角坐标系中,顶点为M的抛物线C:y=ax2+bx与x轴的另一个交点为A(2,0),连接OM、AM,∠OMA=90°.
(1)求抛物线C1的函数表达式;
(2)已知点D的坐标为(0,﹣2),将抛物线C1向上平移得到抛物线C2,抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△DOM与△MAF相似,求所有符合条件的抛物线C2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.

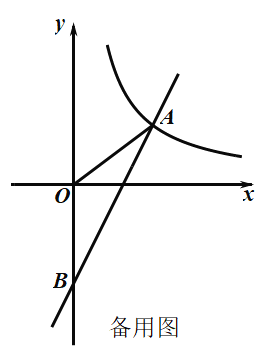
(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
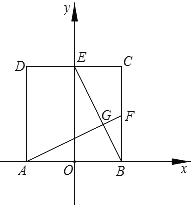
【题目】如图,在正方形ABCD中,顶点A(﹣1,0),C(1,2),点F是BC的中点,CD与y轴交于点E,AF与BE交于点G.将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第99次旋转结束时,点G的坐标为( )
A.(![]() ,
,![]() )B.(﹣
)B.(﹣![]() ,
,![]() )C.(﹣
)C.(﹣![]() ,
,![]() )D.(
)D.(![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现
如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.

填空:
①∠DCE的度数是 ;
②线段CA、CE、CD之间的数量关系是 .
(2)探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
(3)应用
如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情.为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传.某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析,过程如下:
(收集数据)
甲班15名学生测试成绩分别为:78,83,89,97,98,85,100,94,87,90,93,92,99,95;100.
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
(整理数据):
班级 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
甲 | 1 | 1 | 3 | 4 | 6 |
乙 | 1 | 2 | 3 | 5 | 4 |
(分析数据):
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 92 | a | 93 | 47.3 |
乙 | 90 | 87 | b | 50.2 |
(应用数据):
(1)根据以上信息,可以求出:a=_____分,b=______分;
(2)若规定测试成绩92分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,△OAB的边OA在x轴的正半轴上,点B在第二象限,且∠AOB=135°,OA=2,OB=2![]() ,抛物线y=﹣
,抛物线y=﹣![]() x2+bx+c经过点B,并与y轴交于点C(0,5),点P在抛物线的对称轴上.
x2+bx+c经过点B,并与y轴交于点C(0,5),点P在抛物线的对称轴上.
(1)求b、c的值,及抛物线的对称轴.
(2)求证:以点M(2,5)为圆心,半径为2![]() 的圆与边AB相切.
的圆与边AB相切.
(3)若满足条件∠AOB+∠POD=180°与OB:OD=OA:OP的点D恰好在抛物线上,请求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com