
【题目】在图1至图3中,![]() 的直径
的直径![]() ,
,![]() 切
切![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() .
.
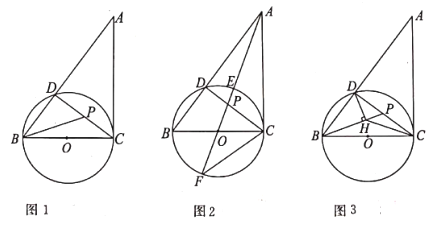
(1)如图1,当点![]() ,
,![]() 的距离最小时,求
的距离最小时,求![]() 的长;
的长;
(2)如图2,若射线![]() 过圆心
过圆心![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如图3,作![]() 于点
于点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)12;(2)![]() ;(3)
;(3)![]() 的最小值为
的最小值为![]()
【解析】
(1)连接![]() ,根据切线的性质和圆周角定理的推论可得
,根据切线的性质和圆周角定理的推论可得![]() ,∠BDC=90°,利用勾股定理求出AB,然后根据三角形的面积公式即可求出CD,根据垂线段最短可得当
,∠BDC=90°,利用勾股定理求出AB,然后根据三角形的面积公式即可求出CD,根据垂线段最短可得当![]() 时,点
时,点![]() ,
,![]() 的距离最小,从而求出PD的长;
的距离最小,从而求出PD的长;
(2)连接![]() ,则
,则![]() ,利用勾股定理即可求出AE,然后根据相似三角形的判定定理证出
,利用勾股定理即可求出AE,然后根据相似三角形的判定定理证出![]() ,列出比例式,根据正切的定义即可求出结论;
,列出比例式,根据正切的定义即可求出结论;
(3)以![]() 为直径作
为直径作![]() ,则
,则![]() 为
为![]() 的中点,利用勾股定理和圆的基本性质求出半径DG,根据直径所对的圆周角是直角可得点H一定在
的中点,利用勾股定理和圆的基本性质求出半径DG,根据直径所对的圆周角是直角可得点H一定在![]() 上,当点
上,当点![]() ,
,![]() ,
,![]() 在一条直线上时,
在一条直线上时,![]() 最小,利用勾股定理求出CG,即可求出结论.
最小,利用勾股定理求出CG,即可求出结论.
解:(1)如图1,连接![]() ,
,
![]() 切
切![]() 于点
于点![]() ,BC为直径
,BC为直径
![]() ,∠BDC=90°
,∠BDC=90°
![]() ,
,![]() ,
,
![]() .
.
由![]() ,
,
即![]() ,
,
解得![]() ,
,
当![]() 时,点
时,点![]() ,
,![]() 的距离最小,此时
的距离最小,此时![]() .
.
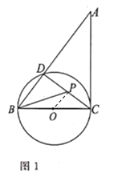
(2)如图2,连接![]() ,则
,则![]() .
.
由(1)知,![]() ,
,
由![]() ,
,
得![]() ,
,
解得![]() .
.
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
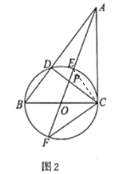
(3)![]() 的最小值为
的最小值为![]() .
.
如图3,以![]() 为直径作
为直径作![]() ,则
,则![]() 为
为![]() 的中点,
的中点,
BD=![]()
∴![]() ,
,
![]() ,
,
∴点![]() 总在
总在![]() 上,
上,![]() ,
,
∴当点![]() ,
,![]() ,
,![]() 在一条直线上时,
在一条直线上时,![]() 最小,
最小,
此时,![]() ,
,
![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
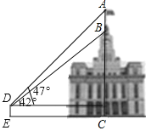
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A、B、C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果精确到0.1m).参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①为了了解一批灯泡的使用寿命,应采用全面调查的方式
②一组数据5,6,7,6, 8,10的众数和中位数都是6
③已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是m≥0
④式子![]() 有意义的条件是
有意义的条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
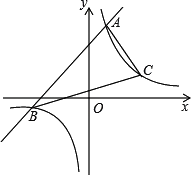
【题目】已知一次函数y1=x+m的图象与反比例函数y2=![]() 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
(1)求一次函数的函数表达式;
(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有独立包装的口罩,其中粉色口罩有3个、蓝色口罩有2个,这些口罩除了颜色外全部相同,从中随机依次不放回拿出两个口罩,则两个口罩都是粉色的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
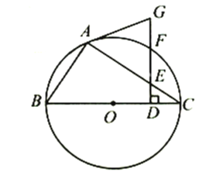
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
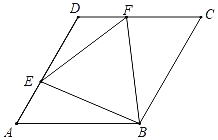
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《水浒传》《三国演义》《西游记》《红楼梦》(按照成书先后顺序)是中国古典长篇小说四大名著.
(1)小黄从这4部名著中,随机选择1部阅读,求他选中《西游记》的概率.
(2)某初中拟从这4部名著中,选择2部作为课外阅读书籍,求《西游记》被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
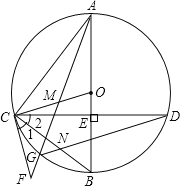
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com