
【题目】已知一次函数y1=x+m的图象与反比例函数y2=![]() 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
(1)求一次函数的函数表达式;
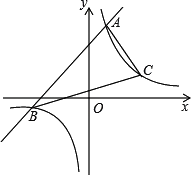
(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积.
【答案】(1)y1=x+5;(2)21.
【解析】
(1)根据当x>1时,y1>y2;当0<x<1时,y1<y2得出点A的横坐标为1,代入反比例解析式中得出A点坐标,再将A点坐标代入一次函数解析式得出m的值;
(2)根据反比例函数在第一象限的图象上有一点C到x轴的距离为2算出C的坐标,再过点C作CD∥x轴交直线AB于D,将三角形ABC的面积分为三角形ACD与三角形BCD的面积之和求算.
(1)∵当x>1时,y1>y2;当0<x<1时,y1<y2
∴点A的横坐标为1
代入反比例函数解析式,![]() =y
=y
解得:y=6
∴点A的坐标为(1,6)
又∵点A在一次函数图象上
∴1+m=6
解得:m=5
∴一次函数的解析式为y1=x+5
(2)∵第一象限内点C到x轴的距离为2
∴点C的纵坐标为2
∴2=![]() ,解得:x=3
,解得:x=3
∴点C的坐标为(3,2)
过点C作CD∥x轴交直线AB于D,
则点D的纵坐标为2
∴x+5=2,
解得:x=﹣3
∴点D的坐标为(﹣3,2)
∴CD=3﹣(﹣3)=3+3=6,
点A到CD的距离为6﹣2=4,
联立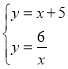
解得: (舍去),
(舍去),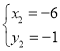
∴点B的坐标为(﹣6,﹣1)
∴点B到CD的距离为2﹣(﹣1)=2+1=3,
S△ABC=S△ACD+S△BCD=![]() ×6×4+
×6×4+![]() ×6×3=12+9=21.
×6×3=12+9=21.



科目:初中数学 来源: 题型:
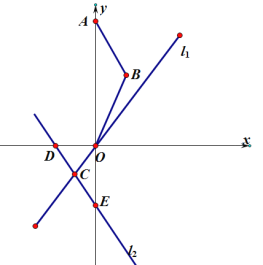
【题目】已知抛物线y=x2+bx+c经过点A(0,6),点B(1,3),直线l1:y=kx(k≠0),直线l2:y=-x-2,直线l1经过抛物线y=x2+bx+c的顶点P,且l1与l2相交于点C,直线l2与x轴、y轴分别交于点D、E.若把抛物线上下平移,使抛物线的顶点在直线l2上(此时抛物线的顶点记为M),再把抛物线左右平移,使抛物线的顶点在直线l1上(此时抛物线的顶点记为N).
(1)求抛物y=x2+bx+c线的解析式.
(2)判断以点N为圆心,半径长为4的圆与直线l2的位置关系,并说明理由.
(3)设点F、H在直线l1上(点H在点F的下方),当△MHF与△OAB相似时,求点F、H的坐标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
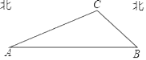
【题目】如图所示,要在某东西走向的A、B两地之间修一条笔直的公路,在公路起点A处测得某农户C在A的北偏东68°方向上.在公路终点B处测得该农户c在点B的北偏西45°方向上.已知A、B两地相距2400米.
(1)求农户c到公路B的距离;(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
(2)现在由于任务紧急,要使该修路工程比原计划提前4天完成,需将该工程原定的工作效率提高20%,求原计划该工程队毎天修路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.
(1)求证:DH是⊙O的切线;
(2)若⊙O的半径为4,AE=FE时,求![]() 的长(结果保留π);
的长(结果保留π);

查看答案和解析>>
科目:初中数学 来源: 题型:
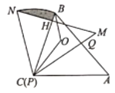
【题目】如图,两个三角形纸板![]() ,
,![]() 能完全重合,
能完全重合,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 从重合位置开始,按逆时针方向旋转,边
从重合位置开始,按逆时针方向旋转,边![]() ,
,![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合),点
重合),点![]() 是
是![]() 的内心,若
的内心,若![]() ,点
,点![]() 运动的路径为
运动的路径为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1至图3中,![]() 的直径
的直径![]() ,
,![]() 切
切![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() .
.
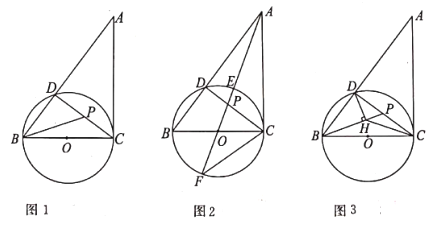
(1)如图1,当点![]() ,
,![]() 的距离最小时,求
的距离最小时,求![]() 的长;
的长;
(2)如图2,若射线![]() 过圆心
过圆心![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如图3,作![]() 于点
于点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
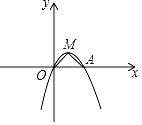
【题目】如图,在平面直角坐标系中,顶点为M的抛物线C:y=ax2+bx与x轴的另一个交点为A(2,0),连接OM、AM,∠OMA=90°.
(1)求抛物线C1的函数表达式;
(2)已知点D的坐标为(0,﹣2),将抛物线C1向上平移得到抛物线C2,抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△DOM与△MAF相似,求所有符合条件的抛物线C2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情.为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传.某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试.现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析,过程如下:
(收集数据)
甲班15名学生测试成绩分别为:78,83,89,97,98,85,100,94,87,90,93,92,99,95;100.
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
(整理数据):
班级 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
甲 | 1 | 1 | 3 | 4 | 6 |
乙 | 1 | 2 | 3 | 5 | 4 |
(分析数据):
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 92 | a | 93 | 47.3 |
乙 | 90 | 87 | b | 50.2 |
(应用数据):
(1)根据以上信息,可以求出:a=_____分,b=______分;
(2)若规定测试成绩92分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com