
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.
(1)求证:DH是⊙O的切线;
(2)若⊙O的半径为4,AE=FE时,求![]() 的长(结果保留π);
的长(结果保留π);

【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由等腰三角形的性质得∠ODB=∠OBD=∠ACB,从而得OD∥AC,进而得DH⊥OD,即可得到结论;
(2)设∠B=∠C=α,由三角形外角的性质得∠EAF=∠EFA=2α,由圆周角定理的推论,得∠E=∠B=α,结合三角形内角和定理,可得α的值,从而可得∠AOD的度数,结合弧长公式,即可求解.
(1)连接OD,
∵OB=OD,
∴△ODB是等腰三角形,∠OBD=∠ODB,
∵在△ABC中, AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是⊙O的切线;
(2)∵AE=EF,
∴∠EAF=∠EFA,
设∠B=∠C=α,
∴∠EAF=∠EFA=2α,
∵∠E=∠B=α,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°,
∴∠AOD=72°,
∴![]() 的长=
的长=![]() =
=![]() .
.



 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】某商场按定价销售某种商品时,每件可获利100元;按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.
(1)该商品进价、定价分别是多少?
(2)该商场用10000元的总金额购进该商品,并在五一节期间以定价的七折优惠全部售出,在每售出一件该商品时,均捐献![]() 元给社会福利事业,该商场为能获得不低于3000元的利润,求
元给社会福利事业,该商场为能获得不低于3000元的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,∠1=15°,则∠2的度数是( )
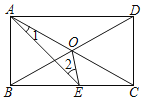
A.25°B.30°C.35°D.15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①为了了解一批灯泡的使用寿命,应采用全面调查的方式
②一组数据5,6,7,6, 8,10的众数和中位数都是6
③已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是m≥0
④式子![]() 有意义的条件是
有意义的条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.

(1)求证:CD为⊙O的切线;
(2)求证:∠C=2∠DBE.
(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
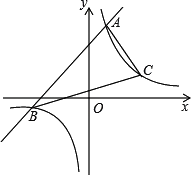
【题目】已知一次函数y1=x+m的图象与反比例函数y2=![]() 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
(1)求一次函数的函数表达式;
(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有独立包装的口罩,其中粉色口罩有3个、蓝色口罩有2个,这些口罩除了颜色外全部相同,从中随机依次不放回拿出两个口罩,则两个口罩都是粉色的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
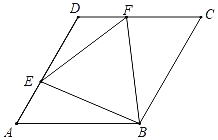
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,0,1,![]() ,
,![]() ,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣
,3这六个数中,随机抽取一个数记为a,则使关于x的二次函数y=x2+(3﹣a)x﹣1在x<﹣1的范围内y随x的增大而减小,且使关于x的分式方程2﹣![]() =
=![]() 的解为正数的a共有( )
的解为正数的a共有( )
A.2个B.3个C.4个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com