
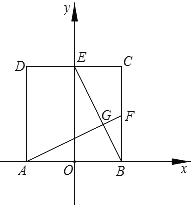
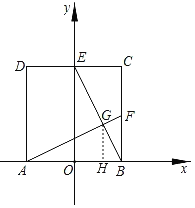
【题目】如图,在正方形ABCD中,顶点A(﹣1,0),C(1,2),点F是BC的中点,CD与y轴交于点E,AF与BE交于点G.将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第99次旋转结束时,点G的坐标为( )
A.(![]() ,
,![]() )B.(﹣
)B.(﹣![]() ,
,![]() )C.(﹣
)C.(﹣![]() ,
,![]() )D.(
)D.(![]() ,﹣
,﹣![]() )
)
【答案】B
【解析】
根据正方形的性质得到AB=BC=CD=2,∠C=∠ABF=90°,根据全等三角形的性质得到∠BAF=∠CBE,根据余角的性质得到∠BGF=90°,过G作GH⊥AB于H,根据相似三角形的性质得到BH=![]() =
=![]() ,求得OH=
,求得OH=![]() ,根据勾股定理得到HG=
,根据勾股定理得到HG=![]() =
=![]() ,求得G(
,求得G(![]() ,
,![]() ),找出规律即可得到结论.
),找出规律即可得到结论.
∵四边形ABCD是正方形,
∴AB=BC=CD=2,∠C=∠ABF=90°,
∵点F是BC的中点,CD与y轴交于点E,
∴CE=BF=1,
∴△ABF≌△BCE(SAS),
∴∠BAF=∠CBE,
∵∠BAF+∠BFA=90°,
∴∠FBG+∠BFG=90°,
∴∠BGF=90°,
∴BE⊥AF,
∵AF=![]() =
=![]() =
=![]() ,
,
∴BG=![]() =
=![]() ,
,
过G作GH⊥AB于H,
∴∠BHG=∠AGB=90°,
∵∠HBG=∠ABG,
∴△ABG∽△GBH,
∴![]() ,
,
∴BG2=BHAB,
∴BH=![]() =
=![]() ,
,
∴OH=![]() ,
,
∵OG=![]() AB=1,
AB=1,
∴HG=![]() =
=![]() ,
,
∴G(![]() ,
,![]() ),
),
∵将正方形ABCD绕点O顺时针每次旋转90°,
∴第一次旋转90°后对应的G点的坐标为(![]() ,﹣
,﹣![]() ),
),
第二次旋转90°后对应的G点的坐标为(﹣![]() ,﹣
,﹣![]() ),
),
第三次旋转90°后对应的G点的坐标为(﹣![]() ,
,![]() ),
),
第四次旋转90°后对应的G点的坐标为(![]() ,
,![]() ),
),
…,
∵99=4×24+3,
∴每4次一个循环,第99次旋转结束时,相当于正方形ABCD绕点O顺时针旋转3次,
∴第99次旋转结束时,点G的坐标为(﹣![]() ,
,![]() ).
).
故选:B.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
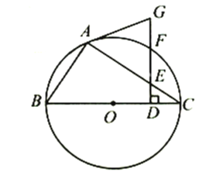
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《水浒传》《三国演义》《西游记》《红楼梦》(按照成书先后顺序)是中国古典长篇小说四大名著.
(1)小黄从这4部名著中,随机选择1部阅读,求他选中《西游记》的概率.
(2)某初中拟从这4部名著中,选择2部作为课外阅读书籍,求《西游记》被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种型号的电风扇,进价及售价如表:
品牌 | A | B |
进价(元/台) | 120 | 180 |
售价(元/台) | 150 | 240 |
(1)该商场4月份用21000元购进A、B两种型号的电风扇,全部售完后获利6000元,求商场4月份购进A、B两种型号电风扇的数量;
(2)该商场5月份计划用不超过42000元购进A、B两种型号电风扇共300台,且B种型号的电风扇不少于50台;销售时准备A种型号的电风扇价格不变,B种型号的电风扇打9折销售.那么商场如何进货才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
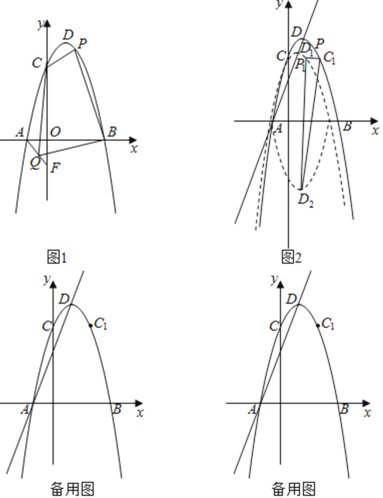
【题目】在平面直角坐标系中,抛物线y=﹣ax2+2ax+c与x轴相交于A(﹣1,0)、B两点(A点在B点左侧),与y轴相交于点C(0,3![]() ),点D是抛物线的顶点.
),点D是抛物线的顶点.
(1)如图1,求抛物线的解析式;
(2)如图1,点F(0,b)在y轴上,连接AF,点Q是线段AF上的一个动点,P是第一象限抛物线上的一个动点,当b=﹣![]() 时,求四边形CQBP面积的最大值与点P的坐标;
时,求四边形CQBP面积的最大值与点P的坐标;
(3)如图2,点C1与点C关于抛物线对称轴对称.将抛物线y沿直线AD平移,平移后的抛物线记为y1,y1的顶点为D1,将抛物线y1沿x轴翻折,翻折后的抛物线记为y2,y2的顶点为D2.在(2)的条件下,点P平移后的对应点为P1,在平移过程中,是否存在以P1D2为腰的等腰△C1P1D2,若存在请直接写出点D2的横坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示8,已知1+2+3+…+n=![]() ,则表示2020的有序数对是( ).
,则表示2020的有序数对是( ).

A.(64,4)B.(65,4)C.(64,61)D.(65,61)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com