
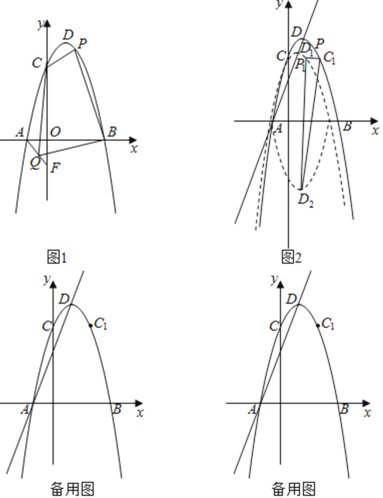
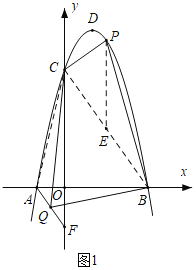
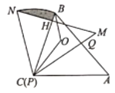
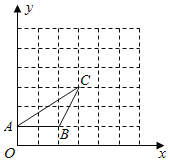
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНЉax2+2ax+cгыxжсЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЁЂBСНЕуЃЈAЕудкBЕузѓВрЃЉЃЌгыyжсЯрНЛгкЕуCЃЈ0ЃЌ3![]() ЃЉЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЎ
ЃЉЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕуFЃЈ0ЃЌbЃЉдкyжсЩЯЃЌСЌНгAFЃЌЕуQЪЧЯпЖЮAFЩЯЕФвЛИіЖЏЕуЃЌPЪЧЕквЛЯѓЯоХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБbЃНЉ![]() ЪБЃЌЧѓЫФБпаЮCQBPУцЛ§ЕФзюДѓжЕгыЕуPЕФзјБъЃЛ
ЪБЃЌЧѓЫФБпаЮCQBPУцЛ§ЕФзюДѓжЕгыЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуC1гыЕуCЙигкХзЮяЯпЖдГЦжсЖдГЦЃЎНЋХзЮяЯпyбижБЯпADЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпМЧЮЊy1ЃЌy1ЕФЖЅЕуЮЊD1ЃЌНЋХзЮяЯпy1биxжсЗелЃЌЗелКѓЕФХзЮяЯпМЧЮЊy2ЃЌy2ЕФЖЅЕуЮЊD2ЃЎдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуPЦНвЦКѓЕФЖдгІЕуЮЊP1ЃЌдкЦНвЦЙ§ГЬжаЃЌЪЧЗёДцдквдP1D2ЮЊбќЕФЕШбќЁїC1P1D2ЃЌШєДцдкЧыжБНгаДГіЕуD2ЕФКсзјБъЃЌШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+2
x2+2![]() x+3
x+3![]() ЃЛЃЈ2ЃЉЕБmЃН
ЃЛЃЈ2ЃЉЕБmЃН![]() ЪБЃЌSЫФБпаЮCQBPШЁЕУзюДѓжЕ
ЪБЃЌSЫФБпаЮCQBPШЁЕУзюДѓжЕ![]() ЃЌДЫЪБPЕузјБъЮЊЃЈ
ЃЌДЫЪБPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкЃЌТњзувЊЧѓЕФD2ЕФКсзјБъгаЃК
ЃЉЃЛЃЈ3ЃЉДцдкЃЌТњзувЊЧѓЕФD2ЕФКсзјБъгаЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋAЁЂCСНЕузјБъДњШыХзЮяЯпНтЮіЪНЕБжаЧѓГіaгыcЕФжЕМДПЩЃЛ
ЃЈ2ЃЉЯШЧѓГіBЁЂFзјБъЃЌШЛКѓПЩвджЄУїAFгыBCЦНааЃЌгкЪЧЁїQBCЕФУцЛ§ОЭЕШгкЁїABCЕФУцЛ§ЃЌЮЪЬтОЭзЊЛЏЮЊЧѓЁїPBCЕФУцЛ§ЕФзюДѓжЕЃЌзїPEЁЮyжсНЛжБЯпBCгкEЃЌЩшPЕуЕФКсзјБъЮЊЮДжЊЪ§mЃЌНЋEЕузјБъвВгУmБэЪОЃЌPEЕФГЄЖШгУPЁЂEзнзјБъжЎВюБэЪОЃЌгкЪЧЁїPBCЕФУцЛ§ОЭПЩвдБэЪОГЩЙигкmЕФЖўДЮКЏЪ§ЃЌЭЈЙ§ХфЗНЗЈМДПЩЧѓГізюжЕМАPЕузјБъЃЎ
ЃЈ3ЃЉгЩгкЯоЖЈСЫвдP1D2ЮЊбќЃЌвђДЫЗжСНДѓРрЗжБ№СаЗНГЬМЦЫуМДПЩЃЎ
ЃЈ1ЃЉНЋAЃЈЉ1ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3![]() ЃЉДњШыХзЮяЯпНтЮіЪНЕУЃК
ЃЉДњШыХзЮяЯпНтЮіЪНЕУЃК
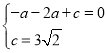
НтЕУЃК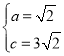 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНЉ![]() x2+2
x2+2![]() x+3
x+3![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгBCЃЌACЃЌзїPEЁЮyжсНЛBCгкEЃЎ
ЁпyЃНЉ![]() x2+2
x2+2![]() x+3
x+3![]() ЃНЉ
ЃНЉ![]() ЃЈx+1ЃЉЃЈxЉ3ЃЉЃЎ
ЃЈx+1ЃЉЃЈxЉ3ЃЉЃЎ
ЁрBЃЈ3ЃЌ0ЃЉЃЌ
ЁпbЃНЉ![]() ЃЌ
ЃЌ
ЁрFЃЈ0ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрAFЁЮBCЃЌ
ЁрSЁїQBCЃНSЁїABCЃН![]() ABOCЃН6
ABOCЃН6![]() ЃЌ
ЃЌ
гЩBЁЂCСНЕузјБъПЩЕУжБЯпBCЕФНтЮіЪНЮЊЃКyЃНЉ![]() x+3
x+3![]() ЃЌ
ЃЌ
ЩшPЃЈmЃЌЉ![]() m2+2
m2+2![]() m+3
m+3![]() ЃЉЃЌдђEЃЈmЃЌЉ
ЃЉЃЌдђEЃЈmЃЌЉ![]() m+3
m+3![]() ЃЉЃЌ
ЃЉЃЌ
PEЃНyPЉyEЃНЉ![]() m2+4
m2+4![]() mЃЌ
mЃЌ
ЁрSЁїPBCЃН![]() ЃЈxBЉxCЃЉЃЈyPЉyEЃЉЃНЉ
ЃЈxBЉxCЃЉЃЈyPЉyEЃЉЃНЉ![]() m2+6
m2+6![]() mЃНЉ
mЃНЉ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрSЫФБпаЮCQBPЃНSЁїQBC+SЁїPBCЃНSЁїABC+SЁїPBCЃНЉ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБmЃН![]() ЪБЃЌSЫФБпаЮCQBPШЁЕУзюДѓжЕ
ЪБЃЌSЫФБпаЮCQBPШЁЕУзюДѓжЕ![]() ЃЌДЫЪБPЕузјБъЮЊЃЈ
ЃЌДЫЪБPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉЁпyЃНЉ![]() x2+2
x2+2![]() x+3
x+3![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDЃЈ1ЃЌ4![]() ЃЉЃЌХзЮяЯпЖдГЦжсЮЊxЃН1ЃЌ
ЃЉЃЌХзЮяЯпЖдГЦжсЮЊxЃН1ЃЌ
ЁпC1гыCЙигкжБЯпxЃН1ЖдГЦЃЌ
ЁрC1ЃЈ2ЃЌ3![]() ЃЉЃЌ
ЃЉЃЌ
гЩAЁЂDСНЕузјБъПЩЧѓЕУжБЯпADЕФНтЮіЪНЮЊyЃН2![]() x+2
x+2![]() ЃЌ
ЃЌ
ЩшD1ЃЈmЃЌ2![]() m+2
m+2![]() ЃЉЃЌ
ЃЉЃЌ
дђP1ЃЈm+![]() ЃЌ2
ЃЌ2![]() m+
m+![]() ЃЉЃЌD2ЃЈmЃЌЉ2
ЃЉЃЌD2ЃЈmЃЌЉ2![]() mЉ2
mЉ2![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЕБP1C1ЃНP1D2ЪБЃЌ![]() ЃН
ЃН![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЕБC1D2ЃНP1D2ЪБЃЌ9m2+36m+54ЃН![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзувЊЧѓЕФD2ЕФКсзјБъгаЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСНИіШ§НЧаЮжНАх![]() ЃЌ
ЃЌ![]() ФмЭъШЋжиКЯЃЌ
ФмЭъШЋжиКЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ДгжиКЯЮЛжУПЊЪМЃЌАДФцЪБеыЗНЯђа§зЊЃЌБп
ДгжиКЯЮЛжУПЊЪМЃЌАДФцЪБеыЗНЯђа§зЊЃЌБп![]() ЃЌ
ЃЌ![]() ЗжБ№гы
ЗжБ№гы![]() ЃЌ
ЃЌ![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЈЕу
ЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌЕу
жиКЯЃЉЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФФкаФЃЌШє
ЕФФкаФЃЌШє![]() ЃЌЕу
ЃЌЕу![]() дЫЖЏЕФТЗОЖЮЊ
дЫЖЏЕФТЗОЖЮЊ![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЖЅЕуAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ1ЃЌ2ЃЉЃЌЕуFЪЧBCЕФжаЕуЃЌCDгыyжсНЛгкЕуEЃЌAFгыBEНЛгкЕуGЃЎНЋе§ЗНаЮABCDШЦЕуOЫГЪБеыа§зЊЃЌУПДЮа§зЊ90ЁуЃЌдђЕк99ДЮа§зЊНсЪјЪБЃЌЕуGЕФзјБъЮЊЃЈЁЁЁЁЃЉ
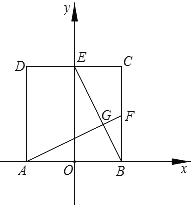
A.ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉB.ЃЈЉ
ЃЉB.ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉC.ЃЈЉ
ЃЉC.ЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉD.ЃЈ
ЃЉD.ЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЦНааЫФБпаЮABCDЕФБпABдкyжсЩЯЃЌЕуDЃЈ4ЃЌ4ЃЉЃЌcosЁЯBCDЃН![]() ЃЌШєЗДБШР§КЏЪ§yЃН
ЃЌШєЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓОЙ§ЦНааЫФБпаЮЖдНЧЯпЕФНЛЕуEЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЃЈkЁй0ЃЉЕФЭМЯѓОЙ§ЦНааЫФБпаЮЖдНЧЯпЕФНЛЕуEЃЌдђkЕФжЕЮЊЃЈ ЃЉ
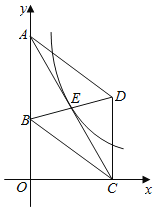
A.14B.7C.8D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020ФъзЂЖЈЪЧВЛЦНЗВЕФвЛФъЃЌаТФъвСЪМЃЌвЛГЁЭЛШчЦфРДЕФвпЧщЯЏОэШЋЙњЃЌШЋЙњШЫУёЭђжквЛаФЃЌПЙеНвпЧщЃЎЮЊСЫдчШеШЁЕУПЙвпЕФЪЄРћЃЌИїМЖеўИЎЁЂИїДѓаТЮХУНЬхЖММгДѓСЫЖдЗРвпжЊЪЖЕФаћДЋЃЎФГаЃЮЊСЫСЫНтГѕвЛФъМЖЙВ480УћЭЌбЇЖдЗРвпжЊЪЖЕФеЦЮеЧщПіЃЌЖдЫћУЧНјааСЫЗРвпжЊЪЖВтЪдЃЎЯжЫцЛњГщШЁМзЁЂввСНАрИї15УћЭЌбЇЕФВтЪдГЩМЈЃЈТњЗж100ЗжЃЉНјааећРэЗжЮіЃЌЙ§ГЬШчЯТЃК
ЃЈЪеМЏЪ§ОнЃЉ
МзАр15УћбЇЩњВтЪдГЩМЈЗжБ№ЮЊЃК78ЃЌ83ЃЌ89ЃЌ97ЃЌ98ЃЌ85ЃЌ100ЃЌ94ЃЌ87ЃЌ90ЃЌ93ЃЌ92ЃЌ99ЃЌ95ЃЛ100ЃЎ
ввАр15УћбЇЩњВтЪдГЩМЈжа90ЁмxЃМ95ЕФГЩМЈШчЯТЃК91ЃЌ92ЃЌ94ЃЌ90ЃЌ93
ЃЈећРэЪ§ОнЃЉЃК
АрМЖ | 75ЁмxЃМ80 | 80ЁмxЃМ85 | 85ЁмxЃМ90 | 90ЁмxЃМ95 | 95ЁмxЃМ100 |
Мз | 1 | 1 | 3 | 4 | 6 |
вв | 1 | 2 | 3 | 5 | 4 |
ЃЈЗжЮіЪ§ОнЃЉЃК
АрМЖ | ЦНОљЪ§ | жкЪ§ | жаЮЛЪ§ | ЗНВю |
Мз | 92 | a | 93 | 47.3 |
вв | 90 | 87 | b | 50.2 |
ЃЈгІгУЪ§ОнЃЉЃК
ЃЈ1ЃЉИљОнвдЩЯаХЯЂЃЌПЩвдЧѓГіЃКaЃН_____ЗжЃЌbЃН______ЗжЃЛ
ЃЈ2ЃЉШєЙцЖЈВтЪдГЩМЈ92ЗжМАЦфвдЩЯЮЊгХауЃЌЧыЙРМЦВЮМгЗРвпжЊЪЖВтЪдЕФ480УћбЇЩњжаГЩМЈЮЊгХауЕФбЇЩњЙВгаЖрЩйШЫЃЛ
ЃЈ3ЃЉИљОнвдЩЯЪ§ОнЃЌФуШЯЮЊФФИіАрЕФбЇЩњЗРвпВтЪдЕФећЬхГЩМЈНЯКУЃПЧыЫЕУїРэгЩЃЈвЛЬѕРэгЩМДПЩЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
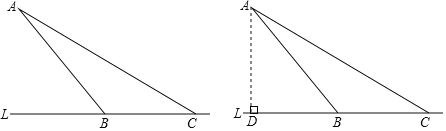
ЁОЬтФПЁПИљОнЕРТЗНЛЭЈЗЈЙцЙцЖЈЃКЦеЭЈЧХСКвЛАуЯоЫй40km/hЃЎЮЊСЫАВШЋЃЌНЛЭЈВПУХдкЧХЭЗЪњСЂОЏЪОХЦЃКЁАЧыЮ№ГЌЫйЁБЃЌВЂМрВтЩуЯёЯЕЭГМрПиЃЌШчЭМЃЌдкФГжБЯпЙЋТЗLТЗЧХЖЮBCФкЯоЫй40km/hЃЌЮЊСЫМьВтГЕСОЪЧЗёГЌЫйЃЌдкОрРыЙЋТЗL500УзХдЕФAДІЩшСЂСЫЙлВтЕуЃЌДгЙлВтЕуAВтЕУвЛаЁГЕДгЕуBЕНДяЕуCааЪЛСЫ30УыжгЃЌвбжЊЁЯABL=45ЁуЃЌЁЯACL=30ЁуЃЌДЫГЕГЌЫйСЫТ№ЃПЧыЫЕУїРэгЩЃЎ(ВЮПМЪ§ОнЃК![]() =1.41ЃЌ
=1.41ЃЌ![]() =1.73)
=1.73)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк5ЁС5ЕФЭјИёжаЃЌКсЁЂзнзјБъОљЮЊећЕуЕФЪ§НазіИёЕуЃЌР§ШчЃЈ0ЃЌ1ЃЉЁЂBЃЈ2ЃЌ1ЃЉЁЂCЃЈ3ЃЌ3ЃЉЖМЪЧИёЕуЃЌЯжНігУЮоПЬЖШЕФжБГпдкЭјИёжазіШчЯТВйзїЃК
ЃЈ1ЃЉжБНгаДГіЕуAЙигкЕуBа§зЊ180ЁуКѓЖдгІЕуMЕФзјБъЁЁ ЁЁЃЛ
ЃЈ2ЃЉЛГіЯпЖЮBEЃЌЪЙBEЁЭACЃЌЦфжаEЪЧИёЕуЃЌВЂаДГіЕуEЕФзјБъЁЁ ЁЁЃЛ
ЃЈ3ЃЉевИёЕуFЃЌЪЙЁЯEAFЃНЁЯCABЃЌЛГіЁЯEAFЃЌВЂаДГіЕуFЕФзјБъЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШбќжБНЧЁїABCЃЌЁЯC=90ЁуЃЌAC=2ЃЌDЮЊБпACЩЯвЛЖЏЕуЃЌСЌНсBDЃЌдкЩфЯпBDЩЯШЁвЛЕуEЪЙBEBD=AB2ЃЎШєЕуDгЩAдЫЖЏЕНCЃЌдђЕуEдЫЖЏЕФТЗОЖГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮOABCжаЃЌЕуOЮЊдЕуЃЌЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§ЕуAЁЂCЃЌгыABНЛгкЕуDЃЎ
x2+bx+cОЙ§ЕуAЁЂCЃЌгыABНЛгкЕуDЃЎ
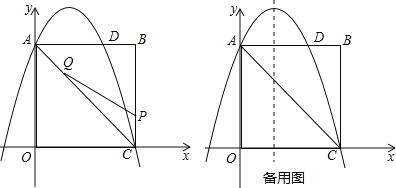
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮBCЩЯвЛИіЖЏЕуЃЈВЛгыЕуCжиКЯЃЉЃЌЕуQЮЊЯпЖЮACЩЯвЛИіЖЏЕуЃЌAQЃНCPЃЌСЌНгPQЃЌЩшCPЃНmЃЌЁїCPQЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкmЕФКЏЪ§БэДяЪНЃЛ
ЂкЕБSзюДѓЪБЃЌдкХзЮяЯпyЃНЉ![]() x2+bx+cЕФЖдГЦжсlЩЯЃЌШєДцдкЕуFЃЌЪЙЁїDFQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
x2+bx+cЕФЖдГЦжсlЩЯЃЌШєДцдкЕуFЃЌЪЙЁїDFQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com