
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AB在y轴上,点D(4,4),cos∠BCD=![]() ,若反比例函数y=
,若反比例函数y=![]() (k≠0)的图象经过平行四边形对角线的交点E,则k的值为( )
(k≠0)的图象经过平行四边形对角线的交点E,则k的值为( )
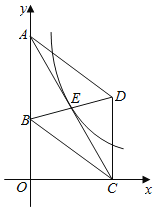
A.14B.7C.8D.![]()
【答案】B
【解析】
过点B作BG⊥CD于点G,根据D(4,4)和勾股定理可得,CG=OB=3,OA=OB+AB=7,过点E作EF⊥x轴于点F,可得EF∥AO,所以EF是三角形AOC的中位线,进而可求EF和OF的长,即可得k的值.
解:如图,过点B作BG⊥CD于点G,

∵D(4,4),
∴DC=OC=BG=4,
∵cos∠BCD=![]() =
=![]() ,
,
∴设CG=3x,则BC=5x,BG=4,
根据勾股定理,得x=1,
∴CG=OB=3,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∴OA=OB+AB=7,
过点E作EF⊥x轴于点F,
∴EF∥AO,
∵平行四边形对角线的交点E,
∴AE=CE,EF∥AO,
∴OF=CF,
∴EF是三角形AOC的中位线,
∴EF=![]() OA=
OA=![]() ,
,
OF=![]() OC=2,
OC=2,
∴k=EFOF=7,
故选:B.


科目:初中数学 来源: 题型:
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种型号的电风扇,进价及售价如表:
品牌 | A | B |
进价(元/台) | 120 | 180 |
售价(元/台) | 150 | 240 |
(1)该商场4月份用21000元购进A、B两种型号的电风扇,全部售完后获利6000元,求商场4月份购进A、B两种型号电风扇的数量;
(2)该商场5月份计划用不超过42000元购进A、B两种型号电风扇共300台,且B种型号的电风扇不少于50台;销售时准备A种型号的电风扇价格不变,B种型号的电风扇打9折销售.那么商场如何进货才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年年初,受新冠肺炎疫情的影响,人们对病毒的防范意识加强,市面上的洗手液也备受欢迎,小王计划购进A型、B型、C型三种洗手液共50箱,其中B型洗手液数量不超过A型洗手液数量,且B型洗手液数量不少于C型洗手液数量的一半.已知A型洗手液每箱60元,B型洗手液每箱80元,C型洗手液每箱100元.在价格不变的条件下,小王实际购进A型洗手液是计划的![]() 倍,C型洗手液购进了12箱,结果小王实际购进三种洗手液共35箱,且比原计划少支付1240元,则小王实际购进B型洗手液_____箱.
倍,C型洗手液购进了12箱,结果小王实际购进三种洗手液共35箱,且比原计划少支付1240元,则小王实际购进B型洗手液_____箱.
查看答案和解析>>
科目:初中数学 来源: 题型:
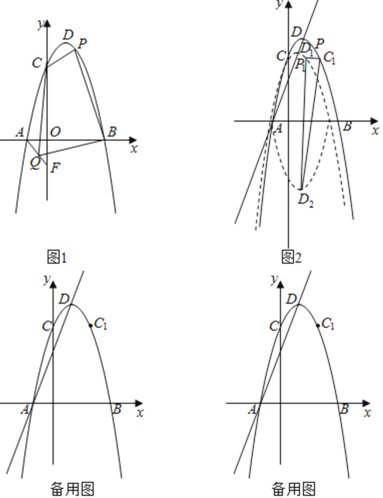
【题目】在平面直角坐标系中,抛物线y=﹣ax2+2ax+c与x轴相交于A(﹣1,0)、B两点(A点在B点左侧),与y轴相交于点C(0,3![]() ),点D是抛物线的顶点.
),点D是抛物线的顶点.
(1)如图1,求抛物线的解析式;
(2)如图1,点F(0,b)在y轴上,连接AF,点Q是线段AF上的一个动点,P是第一象限抛物线上的一个动点,当b=﹣![]() 时,求四边形CQBP面积的最大值与点P的坐标;
时,求四边形CQBP面积的最大值与点P的坐标;
(3)如图2,点C1与点C关于抛物线对称轴对称.将抛物线y沿直线AD平移,平移后的抛物线记为y1,y1的顶点为D1,将抛物线y1沿x轴翻折,翻折后的抛物线记为y2,y2的顶点为D2.在(2)的条件下,点P平移后的对应点为P1,在平移过程中,是否存在以P1D2为腰的等腰△C1P1D2,若存在请直接写出点D2的横坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=a,∠ABC=60°,过点A作AE⊥BC,垂足为E,AF⊥CD,垂足为F.
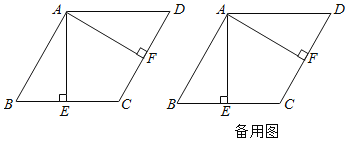
(1)连接EF,用等式表示线段EF与EC的数量关系,并说明理由;
(2)连接BF,过点A作AK⊥BF,垂足为K,求BK的长(用含a的代数式表示);
(3)延长线段CB到G,延长线段DC到H,且BG=CH,连接AG、GH、AH.
①判断△AGH的形状,并说明理由;
②若a=2,S△ADH=![]() (3+
(3+![]() ),求sin∠GAB的值.
),求sin∠GAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).

(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com