
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).

(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)c=3;(2)![]() ;(3)①S=-x2+3x=-(x-
;(3)①S=-x2+3x=-(x-![]() )2+
)2+![]() (1<x<3);当x=
(1<x<3);当x=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() ;②存在点P1(
;②存在点P1(![]() ),或P2(
),或P2(![]() ),此时r1=
),此时r1=![]() ;点P3(
;点P3(![]() ),或P4(
),或P4(![]() ),此时r2=
),此时r2=![]() ,理由见解析.
,理由见解析.
【解析】
(1)将点D(0,3)直接代入解析式即可;
(2)先求出顶点C坐标为(1,4),以及与x轴的交点坐标,即令y=0时,得到点B(3,0)代入一次函数解析式即可求得答案;
(3)根据S=![]() PE·OE,利用P点在线段BC上,可表示出PE,OE,得到S=
PE·OE,利用P点在线段BC上,可表示出PE,OE,得到S=![]() ,变形为顶点式后求出最大值即可.第②小问,根据两圆内切与外切进行分类讨论,分别用r表示出CQ,PQ,CP的长度,再利用勾股定理即可求出r长度和P点坐标.
,变形为顶点式后求出最大值即可.第②小问,根据两圆内切与外切进行分类讨论,分别用r表示出CQ,PQ,CP的长度,再利用勾股定理即可求出r长度和P点坐标.
解:(1)∵将D(0,3)代入解析式
∴c=3
(2)由(1)知抛物线为:
y=-x2+2x+3,配方得y=-(x-1)2+4
∴顶点C坐标为(1,4)
令y=0,得x1=-1,x2=3
∴ B(3,0)
设直线BC解析式为:![]() (
(![]() ),把B、C两点坐标代入,
),把B、C两点坐标代入,
得![]() 解得
解得![]() .
.
∴直线BC解析式为![]()
(3)①∵点P(x,y)在![]() 的图象上,
的图象上,
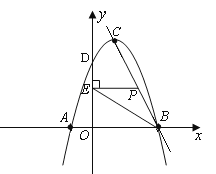
∴PE=x,OE=-2x+6
∴s=![]() PE·OE=
PE·OE=![]()
∴![]()
![]() .
.
∵x=![]() 符合1<x<3,
符合1<x<3,
∴当x=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.
②答:存在.
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2
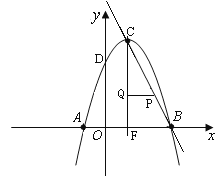
过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴![]() ,即
,即![]()
∴CQ=2r
当⊙P与⊙C外切时,CP=r+1
∵CQ2+PQ2=CP2
∴(2r)2+r2=(r+1)2
解得r=![]() (r=
(r=![]() 舍去)
舍去)
此时P1(![]() ),或P2(
),或P2(![]() )
)
当⊙P与⊙C内切时,CP=r-1.
∵CQ2+PQ2=CP2
∴(2r)2+r2=(r-1)2
解得r=![]() (r=
(r= ![]() 舍去)
舍去)
此时P3(![]() ),或P4(
),或P4(![]() ).
).
∴当r1=![]() , r2=
, r2=![]() 时,⊙P与⊙C相切.
时,⊙P与⊙C相切.
点P的坐标为P1(![]() ),或P2(
),或P2(![]() ),
),
P3(![]() ),或P4(
),或P4(![]() ).
).


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
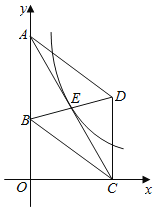
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AB在y轴上,点D(4,4),cos∠BCD=![]() ,若反比例函数y=
,若反比例函数y=![]() (k≠0)的图象经过平行四边形对角线的交点E,则k的值为( )
(k≠0)的图象经过平行四边形对角线的交点E,则k的值为( )
A.14B.7C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰直角△ABC,∠C=90°,AC=2,D为边AC上一动点,连结BD,在射线BD上取一点E使BEBD=AB2.若点D由A运动到C,则点E运动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现
小明在学习鲁教版八年级上册97页例4时,受到启发进行如下数学实验操作:
如图1,取一个锐角为45°的三角尺,把锐角顶点放在正方形ABCD的顶点D处,将三角尺绕点D旋转一个角度,使三角尺的直角边与斜边分别交边AB,BC于点E和点F,连接FE,在绕点D旋转过程中,发现线段AE,EF,CF满足EF=AE+CF的数量关系,但是不会进行证明,数学张老师给他如下的提示:把△ADE绕点D逆时针旋转90°至△DCE’的位置,小明画旋转后的图形,利用全等的知识证明了出来.你根据上面的提示画出旋转后的图形,并将上面的结论进行证明.



问题探究
小明的探究引发了老师的兴趣,老师将三角尺绕点D旋转到如图2的位置,三角尺的直角边与斜边分别交边AB,BC的延长线于点E和点F,老师问题小明此时AE,EF,CF满足什么数量关系,小明思考后说出了正确的结论.请同学们直接写出正确结论(不用写出证明过程).
拓展延伸
张老师让小明利用上面探究积累的学习经验,解答下面的问题:
如图3已知正方形ABCD,点E在边AB上,点F在边BC上,且∠EDF=45°,若CD=6,AE=2,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.
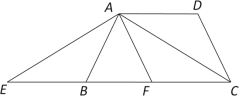
⑴ 求证:AE=AC;
⑵ 若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
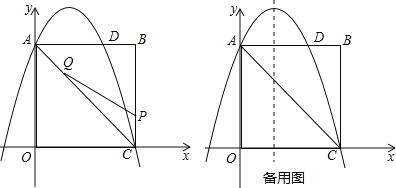
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
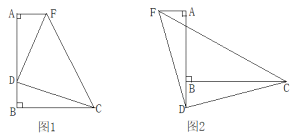
【题目】已知∠ABC=90°,D是直线AB边上的点,AD=BC
(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF的形状并说明理由;
(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小伟一起参加象棋比赛,他们所在的小组共有5名选手.抽签袋里有2红2黑1白共5个小球,摸到同色的成为首轮对手,摸到白球的首轮轮空.现在小组其他3名选手首先依次各摸走一个小球,小亮看到第1个选手摸走的是红球,他对小伟说根据这3名选手的摸球结果我已经知道咱俩恰好首轮对阵的概率了.请你求这个概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com