
【题目】问题发现
小明在学习鲁教版八年级上册97页例4时,受到启发进行如下数学实验操作:
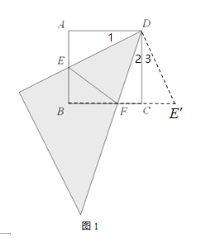
如图1,取一个锐角为45°的三角尺,把锐角顶点放在正方形ABCD的顶点D处,将三角尺绕点D旋转一个角度,使三角尺的直角边与斜边分别交边AB,BC于点E和点F,连接FE,在绕点D旋转过程中,发现线段AE,EF,CF满足EF=AE+CF的数量关系,但是不会进行证明,数学张老师给他如下的提示:把△ADE绕点D逆时针旋转90°至△DCE’的位置,小明画旋转后的图形,利用全等的知识证明了出来.你根据上面的提示画出旋转后的图形,并将上面的结论进行证明.



问题探究
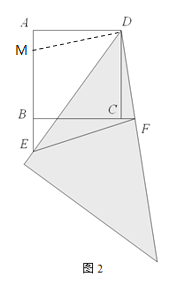
小明的探究引发了老师的兴趣,老师将三角尺绕点D旋转到如图2的位置,三角尺的直角边与斜边分别交边AB,BC的延长线于点E和点F,老师问题小明此时AE,EF,CF满足什么数量关系,小明思考后说出了正确的结论.请同学们直接写出正确结论(不用写出证明过程).
拓展延伸
张老师让小明利用上面探究积累的学习经验,解答下面的问题:
如图3已知正方形ABCD,点E在边AB上,点F在边BC上,且∠EDF=45°,若CD=6,AE=2,求CF的长.
【答案】问题发现:证明见解析;问题探究:AE=CF+EF;拓展延伸:CF的长为:3
【解析】
问题发现
把△ADE绕点逆时针旋转90°至![]() 的位置,可得,
的位置,可得,![]() 由题意可证
由题意可证![]() ,可得.
,可得. ![]() 由
由![]() 则可得EF=AE+CF;
则可得EF=AE+CF;
问题探究
在AB上截取AM=CF,由题意可证△ADM≌△CDF,可得DM=DF,∠ADM=∠CDF,即可得∠EDF=∠MDE=45°,则可证△MDE≌△FDE,可得EF=EM,则可得AE=EF+CF
拓展延伸
在Rt△BEF中, 根据勾股定理可求CF的长.
解:问题发现:
把△ADE绕点D逆时针旋转90°至![]() 的位置
的位置
∴![]()
∴![]()
在正方形ABCD中![]()
∴![]()
∴![]()
∵∠EDF=45°
∴∠1+∠2=45°
∴∠3+∠2=45°
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
问题探究:
如图2:在AB上截取AM=CF,
∵∠A=∠DCF=90°,AM=CF,AD=CD
∴△ADM≌△CDF
∴DM=DF,∠ADM=∠FDC,
∵∠ADM+∠MDC=90°
∴∠CDF+∠MDC=90°,即∠MDF=90°
∵∠EDF=45°
∴∠EDF=
∴△MDE≌△FDE
∴EF=ME
∵AE=AM+ME
∴AE=CF+EF
拓展延伸:
在正方形ABCD中AB=BC=CD=6, ∠EBF=90°
∵AE=2
∴BE=4
设CF=x,则BC=6-x,由(1)可知EF=AE+CF=2+x
在Rt△EBF中:![]()
∴![]()
∴x=3
∴CF的长为:3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,求∠MNA的度数.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠A=90°,D是BC边的中点.
(1)若E在直角边AB上运动,F在直角边AC上运动,在运动过程中始终保持BE=AF.则△EDF_____是三角形.
(2)在(1)的条件下,四边形AEDF的面积是否发生变化?若不变化,请直接写出当AB=4时,四边形AEDF的面积;若变化,请说明理由.
(3)若E,F分别为AB,CA延长线上的点,且BE=AF,其他条件不变,那么(1)中的结论是否还成立?画图并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
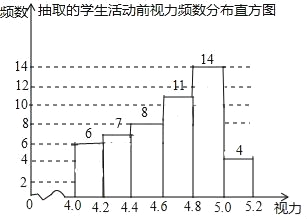
【题目】为了保护视力,某学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示,(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表格所示.
抽取的学生活动后视力频数分布表
分组 | 频数 |
4.0≤x<4.2 | 2 |
4.2≤x<4.4 | 4 |
4.4≤x<4.6 | 6 |
4.6≤x<4.8 | 10 |
4.8≤x<5.0 | 21 |
5.0≤x<5.2 | 7 |
(1)此次调查所抽取的样本容量为 ;
(2)若视力达到4.8以上(含4.8)为达标,请估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为( )

A. (﹣4,﹣5) B. (﹣5,﹣4) C. (﹣3,﹣4) D. (﹣4,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,

(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个一次函数l1、l2的图象如图:

(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com