
【题目】如图,在等腰三角形ABC中,∠A=90°,D是BC边的中点.
(1)若E在直角边AB上运动,F在直角边AC上运动,在运动过程中始终保持BE=AF.则△EDF_____是三角形.
(2)在(1)的条件下,四边形AEDF的面积是否发生变化?若不变化,请直接写出当AB=4时,四边形AEDF的面积;若变化,请说明理由.
(3)若E,F分别为AB,CA延长线上的点,且BE=AF,其他条件不变,那么(1)中的结论是否还成立?画图并证明你的结论.

【答案】(1)等腰直角;(2)四边形AEDF面积不变;(3)成立,证明见解析.
【解析】
(1)题要通过构建全等三角形来求解.连接AD,可通过证△ADF和△BDE全等来求本题的结论.
(2)题可把将四边形AEDF的面积分成△ADF和ADE的面积和求解,由(1)证得△ADF和△BDE全等,因此四边形AEDF的面积可转化为△ABD的面积,由此得证.
(3)与(1)题的思路和解法一样.
(1)证明:如图1中,连接AD.

∵AB=AC,∠A=90°,D为BC中点
∴AD=![]() =BD=CD
=BD=CD
且AD平分∠BAC
∴∠BAD=∠CAD=45°
在△BDE和△ADF中,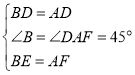 ,
,
∴△BDE≌△ADF(SAS)
∴DE=DF,∠BDE=∠ADF
∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
故答案为等腰直角.
(2)解:四边形AEDF面积不变.
理由:∵由(1)可知,△AFD≌△BED,
∴S△BDE=S△ADF,
而S四边形AEDF=S△AED+S△ADF=S△AED+S△BDE=S△ABD
∴S四边形AEDF不会发生变化.
(3)解:仍为等腰直角三角形.
理由:如图2中,连接AD.
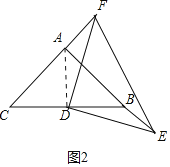
∵△AFD≌△BED,
∴DF=DE,∠ADF=∠BDE,
∵∠ADF+∠FDB=90°,
∴∠BDE+∠FDB=90°,
即:∠EDF=90°,
∴△EDF为等腰直角三角形.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=2,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中.
中.
![]() 利用尺规作图,在BC边上求作一点P,使得点P到AB的距离
利用尺规作图,在BC边上求作一点P,使得点P到AB的距离![]() 的长
的长![]() 等于PC的长;
等于PC的长;
![]() 利用尺规作图,作出
利用尺规作图,作出![]() 中的线段PD.
中的线段PD.
![]() 要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑
要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且CE=DF.
(1)求证:AB=AC.
(2)如果∠ABD=105°,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在x轴的正半轴上,点B在反比例函数y=![]() (k>0,x>0)的图象上,延长AB交该函数图象于另一点C,BC=3AB,点D也在该函数的图象上,BD=BC,以BC,BD为边构造CBDE,若点O,B,E在同一条直线上,且CBDE的周长为k,则AB的长为_____.
(k>0,x>0)的图象上,延长AB交该函数图象于另一点C,BC=3AB,点D也在该函数的图象上,BD=BC,以BC,BD为边构造CBDE,若点O,B,E在同一条直线上,且CBDE的周长为k,则AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现
小明在学习鲁教版八年级上册97页例4时,受到启发进行如下数学实验操作:
如图1,取一个锐角为45°的三角尺,把锐角顶点放在正方形ABCD的顶点D处,将三角尺绕点D旋转一个角度,使三角尺的直角边与斜边分别交边AB,BC于点E和点F,连接FE,在绕点D旋转过程中,发现线段AE,EF,CF满足EF=AE+CF的数量关系,但是不会进行证明,数学张老师给他如下的提示:把△ADE绕点D逆时针旋转90°至△DCE’的位置,小明画旋转后的图形,利用全等的知识证明了出来.你根据上面的提示画出旋转后的图形,并将上面的结论进行证明.



问题探究
小明的探究引发了老师的兴趣,老师将三角尺绕点D旋转到如图2的位置,三角尺的直角边与斜边分别交边AB,BC的延长线于点E和点F,老师问题小明此时AE,EF,CF满足什么数量关系,小明思考后说出了正确的结论.请同学们直接写出正确结论(不用写出证明过程).
拓展延伸
张老师让小明利用上面探究积累的学习经验,解答下面的问题:
如图3已知正方形ABCD,点E在边AB上,点F在边BC上,且∠EDF=45°,若CD=6,AE=2,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
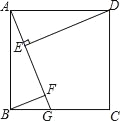
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)如图1,求证:AE=BF;
(2)连接DF,若tan∠BAG=![]() ,AB=2
,AB=2![]() ,求△ADF的面积.
,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com