练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

    （1）求证：△ACD≌△AED；

    （2）若∠B=30°，CD=2，求BD的长．

    【答案】（1）证明见解析；（2）BD=4．

    【解析】

    （1）根据角平分线性质求出CD=DE，根据HL定理求出另三角形全等即可；
    （2）求出∠DEB=90°，DE=2，根据含30度角的直角三角形性质求出即可．

    （1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，

    ∴CD=ED，∠DEA=∠C=90°，

    ∵在Rt△ACD和Rt△AED中，

    ，

    ∴Rt△ACD≌Rt△AED（HL）；

    （2）∵DC=DE=2，DE⊥AB，

    ∴∠DEB=90°，

    ∵∠B=30°，

    ∴BD=2DE=4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】炮弹的运行轨道若不计空气阻力是一条抛物线．现测得我军炮位A与射击目标B的水平距离为600m，炮弹运行的最大高度为1200m.

    (1)求此抛物线的解析式；

    (2)若在A、B之间距离A点500m处有一高350m的障碍物，计算炮弹能否越过障碍物.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

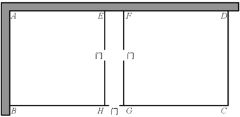
    【题目】某农场要建一个饲养场（矩形ABCD）两面靠现有墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）。建成后木栏总长45米。设饲养场（矩形ABCD）的一边AB长为x米.

    （1）饲养场另一边BC= 米（用含x的代数式表示）.

    （2）若饲养场的面积为180平方米，求x的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校“体育课外活动兴趣小组”，开设了以下体育课外活动项目：A．足球 B．乒乓球C．羽毛球 D．篮球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

    （1）这次被调查的学生共有　 　人，在扇形统计图中“D”对应的圆心角的度数为　 　；

    （2）请你将条形统计图补充完整；

    （3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加市里组织的乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．

    （1）求证：AB=CF；

    （2）连接DE，若AD=2AB，求证：DE⊥AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图， △ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC

    ⑴求∠ECD的度数；

    ⑵若CE=5，求CB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于M，交AC于N．

    （1）若∠ABC=70°，求∠MNA的度数．

    （2）连接NB，若AB=8cm，△NBC的周长是14cm．求BC的长；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的角平分线，添加下列条件能使△ABD≌△ACD的是（ ）

    ①AB＝AC；②AB＝AD；③∠ADB＝90°；④BD＝CD.

    A.①②③B.①②④C.①③D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰三角形ABC中，∠A＝90°，D是BC边的中点.

    (1)若E在直角边AB上运动，F在直角边AC上运动，在运动过程中始终保持BE＝AF.则△EDF_____是三角形.

    (2)在(1)的条件下，四边形AEDF的面积是否发生变化？若不变化，请直接写出当AB＝4时，四边形AEDF的面积；若变化，请说明理由.

    (3)若E，F分别为AB，CA延长线上的点，且BE＝AF，其他条件不变，那么(1)中的结论是否还成立？画图并证明你的结论.

    查看答案和解析>>

    同步练习册答案