
����Ŀ����ͼ��������ABCD�У�AB��a����ABC��60�㣬����A��AE��BC������ΪE��AF��CD������ΪF��
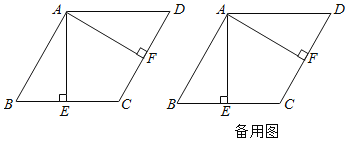
��1������EF���õ�ʽ��ʾ�߶�EF��EC��������ϵ����˵�����ɣ�
��2������BF������A��AK��BF������ΪK����BK�ij����ú�a�Ĵ���ʽ��ʾ����
��3���ӳ��߶�CB��G���ӳ��߶�DC��H����BG��CH������AG��GH��AH��
���жϡ�AGH����״����˵�����ɣ�
����a��2��S��ADH��![]() ��3+
��3+![]() ������sin��GAB��ֵ��
������sin��GAB��ֵ��
���𰸡���1��EF��![]() EC�����ɼ���������2��BK��
EC�����ɼ���������2��BK��![]() ����3������AGHΪ�ȱ������Σ����ɼ���������sin��GAB��
����3������AGHΪ�ȱ������Σ����ɼ���������sin��GAB��![]() ��
��
��������
(1)�������ε����ʵó��߶κͽǶ����,�����Ƴ���AEB�ա�AFD,��ͨ������֤����AEFΪ�ȱ�������,���ݵȱ������ε��������EF����.
(2)�������Ǻ������BK����.
(3)�ٸ������⻭��ͼ��,����������ȫ��֤���������һ��Ϊ60�㼴��֤����AGHΪ�ȱ�������;�ڹ���C��CM��AH�ڵ�M,ͨ����ADH��������DH,�Ӷ����CH��HF,��֤����AFH�ǵ���ֱ��������,���������Ǻ����������.
������ABCD�У���ABC��60�㣬���ABC����ACDΪ�����߳�Ϊa�ĵȱ������Σ�
��1����ͼ1����AB��AD����ABE����ADF����ADF����AEB��90�㣬
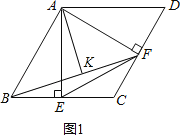
���AEB�ա�AFD��AAS����
��AE��AF��
�ڵȱߡ�ABC�У���AE��BC��
��AE�ǡ�BAC�Ľ�ƽ���ߣ��ʡ�BAE��30�㣬
ͬ����DAF��30�㣬
�ߡ�ABC��60�㣬���BAD��120�㣬
���EAF����BAD����BAE����DAF��120�㩁30�㩁30�㣽60�㣬
���AEFΪ�ȱ������Σ�
�ڵȱ�������ABC�У�AE��ABsin��ABC��![]() a��EF��AF��BE��EC��
a��EF��AF��BE��EC��![]() a��
a��
��EF��![]() EC��
EC��
��2����ͼ1����BAF����BAD����FAD��90�㣬
��Rt��ABF��tan��ABF��![]() ��
��![]() ��
��![]() ����cos��ABF��
����cos��ABF��![]() ��
��
��Rt��ABK��BK��ABcos��ABF��a��![]() ��
��![]() a��
a��
��3������ͼ2������AC��
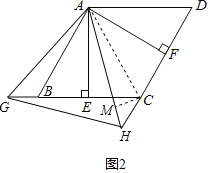
��BG��CH��AB��AC��
�֡ߡ�ABG��180�㩁��ABC��120�㣬��ACH��180�㩁ACD��120�㣽��ABG��
���ABG�ա�ACH��SAS����
��AG��AH����GAB����HAC��
���GAH����GAB+��BAH����HAC+��BAH����BAC��60�㣬
���AGHΪ�ȱ������Σ�
����ͼ2������C��CM��AH�ڵ�M��
S��ADH��![]() AF��DH��
AF��DH��![]() ��
��![]() ��2��DH��
��2��DH��![]() ��3+
��3+![]() ����
����
��ã�DH��![]() ��
��
CH��DH��CD��![]() ��
��
HF��DH��FD��![]() ��AF��
��AF��
���AFHΪ����ֱ�������Σ����AHC��45�㣬
��Rt��CHM��sin��MHC��![]() ��
��![]() ��sin45�㣽
��sin45�㣽![]() ��
��
��CM��![]() ��
��
��Rt��ACM��sin��HCM��![]() ��
��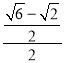 ��
��![]() ��sin��GAB��
��sin��GAB��
��sin��GAB��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⷢ�֣�
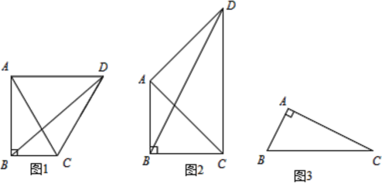
��1����ͼ1����Rt��ABC�У���BAC=30�㣬��ABC��90�㣬���߶�AC�Ƶ�A��ʱ����ת����ת����=2��BAC�� ��BCD�Ķ������������߶�BD��AC֮���������ϵ��������
���̽����
��2����Rt��ABC�У���BAC=45�㣬��ABC��90�㣬���߶�AC�Ƶ�A��ʱ����ת����ת����=2��BAC�����ʣ�1���еĽ��ۻ������𣿣�
��չ���죺
��3����ͼ3����Rt��ABC�У�AB��2��AC��4����BDC��90�㣬����P����PB��PC����BPC��90�㣬��ֱ��д���߶�AP�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
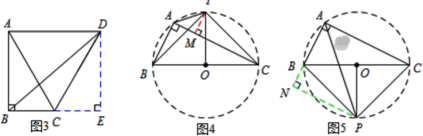
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ƽ���ı���ABCD�ı�AB��y���ϣ���D��4��4����cos��BCD��![]() ��������������y��
��������������y��![]() ��k��0����ͼ��ƽ���ı��ζԽ��ߵĽ���E����k��ֵΪ�� ��
��k��0����ͼ��ƽ���ı��ζԽ��ߵĽ���E����k��ֵΪ�� ��
A.14B.7C.8D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
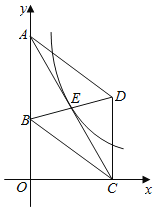
����Ŀ�����ݵ�·��ͨ����涨����ͨ����һ������40km/h��Ϊ�˰�ȫ����ͨ��������ͷ������ʾ�ƣ��������١������������ϵͳ��أ���ͼ����ijֱ�߹�·L·�Ŷ�BC������40km/h��Ϊ�˼����Ƿ��٣��ھ��빫·L500���Ե�A�������˹۲�㣬�ӹ۲��A���һС���ӵ�B�����C��ʻ��30���ӣ���֪��ABL=45�㣬��ACL=30�㣬�˳�����������˵�����ɣ�(�ο����ݣ�![]() =1.41��
=1.41��![]() =1.73)
=1.73)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����5��5�������У��ᡢ�������Ϊ�������������㣬���磨0��1����B��2��1����C��3��3�����Ǹ�㣬�ֽ����̶ȵ�ֱ���������������²�����
��1��ֱ��д����A���ڵ�B��ת180����Ӧ��M�������� ����
��2�������߶�BE��ʹBE��AC������E�Ǹ�㣬��д����E�������� ����
��3���Ҹ��F��ʹ��EAF����CAB��������EAF����д����F�������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
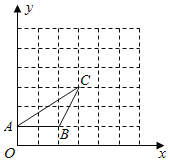
����Ŀ����ͼ������ABC�У���ABC��90����AB��BC�������εĶ������ƽ�е�����ֱ��l1��l2��l3�ϣ���l1��l2֮��ľ���Ϊ2��l2��l3֮��ľ���Ϊ3��BC��l2��D�㣮
��1����AB�ij���
��2����sin��BAD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ֱ�ǡ�ABC����C=90����AC=2��DΪ��AC��һ���㣬����BD��������BD��ȡһ��EʹBEBD=AB2������D��A�˶���C�����E�˶���·����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⷢ��
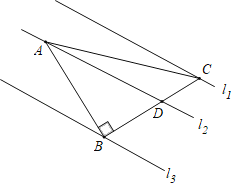
С����ѧϰ³�̰���꼶�ϲ�97ҳ��4ʱ,�ܵ���������������ѧʵ�����:
��ͼ1,ȡһ�����Ϊ45�������dz�,����Ƕ������������ABCD�Ķ���D���������dz��Ƶ�D��תһ���Ƕ�,ʹ���dzߵ�ֱ�DZ���б�߷ֱ�AB,BC�ڵ�E�͵�F,����FE,���Ƶ�D��ת������,�����߶�AE,EF,CF����EF=AE+CF��������ϵ,���Dz������֤��,��ѧ����ʦ�������µ���ʾ:����ADE�Ƶ�D��ʱ����ת90������DCE����λ��,С������ת���ͼ��,����ȫ�ȵ�֪ʶ֤���˳���.������������ʾ������ת���ͼ��,��������Ľ��۽���֤��.



����̽��
С����̽����������ʦ����Ȥ,��ʦ�����dz��Ƶ�D��ת����ͼ2��λ��,���dzߵ�ֱ�DZ���б�߷ֱ�AB,BC���ӳ����ڵ�E�͵�F,��ʦ����С����ʱAE,EF,CF����ʲô������ϵ,С��˼����˵������ȷ�Ľ���.��ͬѧ��ֱ��д����ȷ����(����д��֤������).
��չ����
����ʦ��С����������̽�����۵�ѧϰ����,������������:
��ͼ3��֪������ABCD,��E�ڱ�AB��,��F�ڱ�BC��,�ҡ�EDF=45��,��CD=6,AE=2,��CF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
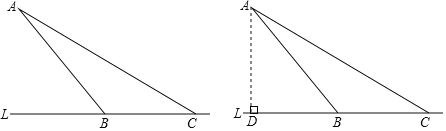
����Ŀ����֪��ABC=90�㣬D��ֱ��AB���ϵĵ㣬AD=BC
��1����ͼ1����D���߶�AB�ϣ�����A��AF��AB����AF=BD������DC��DF��CF�����жϡ�CDF����״��˵�����ɣ�
��2����ͼ2����D���߶�AB���ӳ����ϣ���F�ڵ�A����࣬�����������䣬���Ͻ����Ƿ���Ȼ��������˵�����ɣ�
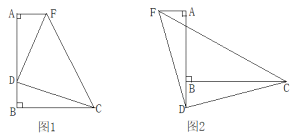
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com