
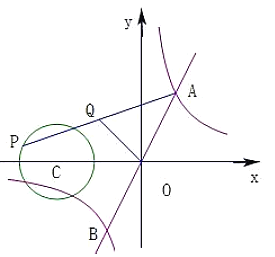
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,点
,点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的⊙
为半径的⊙![]() 上,
上,![]() 是
是![]() 的中点,若
的中点,若![]() 长的最大值为
长的最大值为![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】![]()
【解析】
由三角形中位线的性质可知BP长的最大值为3,此时BP过圆心C,过B作BD⊥x轴于D,设B(t,2t),则CD= t+2,BD=2t,在Rt△BCD中,根据勾股定理即可求得t的值,再根据反比例函数图像上点的坐标特征即可求出k的值.
连接BP,
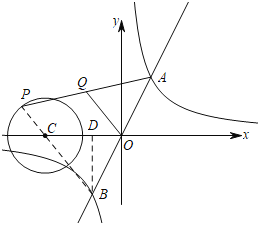
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=12BP,
∵OQ长的最大值为![]() ,
,
∴BP长的最大值为![]() ×2=3,
×2=3,
如图,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t(2)=t+2,BD=2t,
在Rt△BCD中,由勾股定理得:;BC2=CD2+BD2,
∴22=(t+2)2+(2t)2,
t=0(舍)或![]() ,
,
∴B(![]() ,
,![]() ),
),
∵点B在反比例函数y=![]() (k>0)的图象上,
(k>0)的图象上,
∴k=![]() ×(
×(![]() )=
)=![]() ;
;
故答案为![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,以扇形 OAB 的顶点 O 为原点,半径 OB 所在的直线为 x 轴,建立平面直角坐标系,点 B 的坐标为(2,0),若抛物线 ![]() (n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )
(n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )

A.n>-4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y= ![]() +(1-2a)x(a>0),下列说法错误的是( )
+(1-2a)x(a>0),下列说法错误的是( )
A. 当![]() 时,该二次函数图象的对称轴为y轴
时,该二次函数图象的对称轴为y轴
B. 当a>![]() 时,该二次函数图象的对称轴在y轴的右侧
时,该二次函数图象的对称轴在y轴的右侧
C. 该二次函数的图象的对称轴可为x=1
D. 当x>2时,y的值随x的值增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
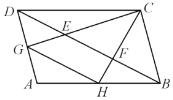
【题目】如图,![]() ,
,![]() 是平行四边形
是平行四边形![]() 从对角线
从对角线![]() 上的两点,
上的两点,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的关系正确的是( )
的关系正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 是直径,点
是直径,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 边于点
边于点![]() .
.
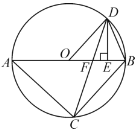
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() ,求四边形
,求四边形![]() 的面积(用含有
的面积(用含有![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,∠CAF=2∠B.
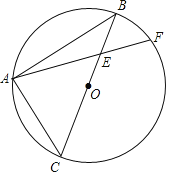
(1)求证:AE=AC;
(2)若⊙O的半径为4,E是OB的中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生获取信息的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图,该调查的方式和图中a的值分别是( )

A. 抽样调查,24 B. 普查,24 C. 抽样调查,26 D. 普查,26
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com