
【题目】如图,小明在水平面E处,测得某建筑物AB的顶端A的仰角为42°,向正前方向走37米到达点D处,再往斜坡CD上走30米到达点C处,测得建筑物AB的顶端A的仰角为63.5°,已知斜坡CD的坡度为i=1:0.75,建筑物AB垂直于平台BC,平台BC与水平面DE平行,点A、B、C、D、E均在同一平面内,则建筑物AB的高度约为( )(精确到0.1米,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.0)
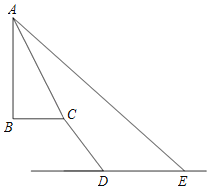
A.42.4米B.46.4米C.48.5米D.50.8米
【答案】B
【解析】
作CG⊥DE交ED的延长线于G,延长AB交ED的延长线于H,根据坡度的概念分别求出CG、DG,根据正切的定义用AB表示出BC,根据正切的定义列式计算,得到答案.
解:作CG⊥DE交ED的延长线于G,延长AB交ED的延长线于H,
则四边形BHGC为矩形,
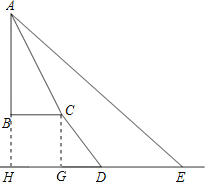
∴BH=CG,BC=HG,
设CG=x米,
∵斜坡CD的坡度为i=1:0.75,
∴DG=3x,
由勾股定理得,CD2=CG2+DG2,即302=(4x)2+(3x)2,
解得,x=6,
∴CG=24,DG=18,
在Rt△ABC中,tan∠ACB=![]() ,
,
∴BC=![]() ,
,
在Rt△AHE中,tan∠AEH=![]()
∴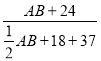 ≈0.9,
≈0.9,
解得,AB≈46.4,
故选:B.


科目:初中数学 来源: 题型:
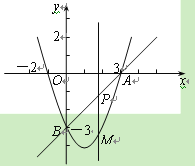
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
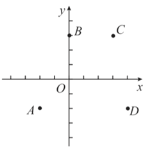
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A、B(点A在点B的左侧),且AB=6.
轴交于点A、B(点A在点B的左侧),且AB=6.
(1)求这条抛物线的对称轴及表达式;
(2)在y轴上取点E(0,2),点F为第一象限内抛物线上一点,联结BF、EF,如果![]() ,求点F的坐标;
,求点F的坐标;
(3)在第(2)小题的条件下,点F在抛物线对称轴右侧,点P在![]() 轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.
轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
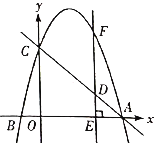
【题目】如图,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的解析式.
(2)点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,求线段
,求线段![]() 的长度最大值.
的长度最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
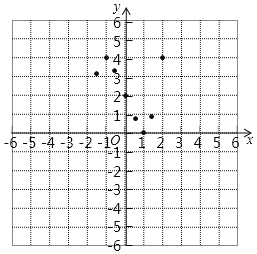
【题目】在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时 y=0.
(1)根据已知条件可知这个函数的表达式 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
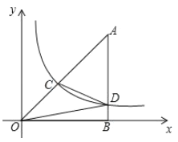
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 位于第一象限,点
位于第一象限,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴正半轴上,若双曲线
轴正半轴上,若双曲线![]()
![]() 与
与![]() 的边
的边![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
、![]() .若
.若![]() ,则
,则![]() 为_______________.
为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校旗杆的下方有一块圆形草坪,草坪的外面围着“圆环”水池,草坪和水池的外边缘是两个同心圆,旗杆在圆心O的位置且与地面垂直.
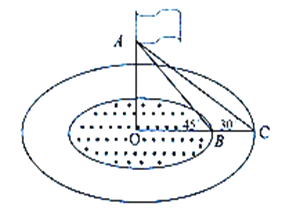
(1)若草坪的面积与圆环水池的面积之比为1∶4,求两个同心圆的半径之比.
(2)如图,若水池外面通往草坪有一座10米长的小桥BC,小桥所在的直线经过圆心O,上午8:00时太阳光线与地面成30°角,旗杆顶端的影子恰好落在水池的外缘;上午9:00时太阳光线与地面成45°角,旗杆顶端的影子恰好落在草坪的外缘,求旗杆的高OA长.
查看答案和解析>>
科目:初中数学 来源: 题型:
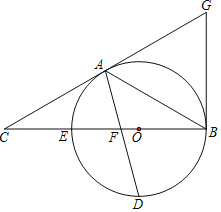
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC,
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
(3)过点B作⊙O的切线交CA的延长线于G,如果连接AE,将线段AC以直线AE为对称轴作对称线段AH,点H正好落在⊙O上,连接BH,求证:四边形AHBG为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com