
ЁОЬтФПЁПдкбЇЯАКЏЪ§ЕФЙ§ГЬжаЃЌЮвУЧОРњСЫЁАШЗЖЈКЏЪ§ЕФБэДяЪНЉЉРћгУКЏЪ§ЭМЯѓбаОПЦфаджЪЉЉдЫгУКЏЪ§НтОіЮЪЬтЁБЕФбЇЯАЙ§ГЬЃЌИљОнФуЫљОРњЕФбЇЯАЙ§ГЬЃЌЯждкРДНтОіЯТУцЕФЮЪЬтЃКдкКЏЪ§yЃНax3Љbx+2жаЃЌЕБxЃНЉ1ЪБЃЌyЃН4ЃЛЕБxЃНЉ2ЪБ yЃН0ЃЎ
ЃЈ1ЃЉИљОнвбжЊЬѕМўПЩжЊетИіКЏЪ§ЕФБэДяЪНЁЁ ЁЁЃЎ
ЃЈ2ЃЉИљОнвбУшГіЕФВПЗжЕуЃЌЛГіИУКЏЪ§ЭМЯѓЃЎ
ЃЈ3ЃЉЙлВьЫљЛЭМЯѓЃЌЛиД№ЯТСаЮЪЬтЃК
ЂйИУЭМЯѓЙигкЕуЁЁ ЁЁГЩжааФЖдГЦЃЛ
ЂкЕБxШЁКЮжЕЪБЃЌyЫцзХxЕФдіДѓЖјМѕаЁЃЛ
ЂлШєжБЯпyЃНcгыИУЭМЯѓга3ИіНЛЕуЃЌжБНгаДГіcЕФШЁжЕЗЖЮЇЃЎ
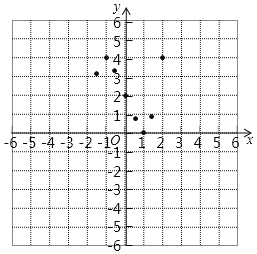
ЁОД№АИЁПЃЈ1ЃЉyЃНx3Љ3x+2ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂй(0ЃЌ-2)ЃЛЂкЉ1ЃМxЃМ1ЃЛЂл0ЃМcЃМ4
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈНтОіЮЪЬтМДПЩЃЎ
ЃЈ2ЃЉРћгУУшЕуЗЈЛГіКЏЪ§ЭМЯѓМДПЩЃЎ
ЃЈ3ЃЉРћгУЪ§аЮНсКЯЕФЫМЯыНтОіЮЪЬтМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрКЏЪ§НтЮіЪНЮЊЃКyЃНx3Љ3x+2ЃЎ
ЙЪД№АИЮЊЃКyЃНx3Љ3x+2ЃЎ
ЃЈ2ЃЉКЏЪ§ЭМЯѓШчЭМЫљЪОЃК

ЃЈ3ЃЉЂйЙлВьЭМЯѓПЩжЊЃККЏЪ§ЭМЯѓЙигкЃЈ0ЃЌ2ЃЉГЩжааФЖдГЦЃЎ
ЙЪД№АИЮЊЃКЃЈ0ЃЌЉ2ЃЉЃЎ
ЂкЙлВьЭМЯѓПЩжЊЃКЕБЉ1ЃМxЃМ1ЪБЃЌyЫцзХxЕФдіДѓЖјМѕаЁЃЎ
ЂлЙлВьЭМЯѓПЩжЊЃКШєжБЯпyЃНcгыИУЭМЯѓга3ИіНЛЕуЃЌcЕФШЁжЕЗЖЮЇЮЊ0ЃМcЃМ4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌдђдкЯТСаИїЪНзгЃКЂйabc>0ЃЛЂкa+b+c>0ЃЛЂлa+c>bЃЛЂм2a+b=0ЃЛЂн![]() =b2-4ac<0жаЃЌГЩСЂЕФЪНзгга( )
=b2-4ac<0жаЃЌГЩСЂЕФЪНзгга( )
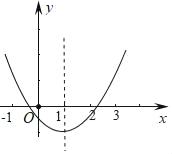
A. ЂкЂмЂн B. ЂкЂлЂн
C. ЂйЂкЂм D. ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌДцдкХзЮяЯп
жаЃЌДцдкХзЮяЯп![]() вдМАСНЕу
вдМАСНЕу![]() КЭ
КЭ![]() .
.
(1)ЧѓИУХзЮяЯпЕФЖЅЕузјБъ;
(2)ШєИУХзЮяЯпОЙ§Еу![]() ЃЌЧѓДЫХзЮяЯпЕФБэДяЪН;
ЃЌЧѓДЫХзЮяЯпЕФБэДяЪН;
(3)ШєИУХзЮяЯпгыЯпЖЮ![]() жЛгавЛИіЙЋЙВЕуЃЌНсКЯЭМЯѓЃЌЧѓ
жЛгавЛИіЙЋЙВЕуЃЌНсКЯЭМЯѓЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЗХжУгкЦНУцжБНЧзјБъЯЕжаЃЌАДЯТУцвЊЧѓЛЭМЃК
ЗХжУгкЦНУцжБНЧзјБъЯЕжаЃЌАДЯТУцвЊЧѓЛЭМЃК
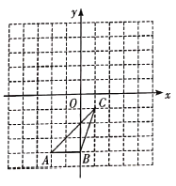
ЃЈ1ЃЉЛГі![]() ШЦдЕу
ШЦдЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕФ
ЕФ![]() .
.
ЃЈ2ЃЉЧѓЕу![]() дка§зЊЙ§ГЬжаЕФТЗОЖГЄЖШ.
дка§зЊЙ§ГЬжаЕФТЗОЖГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁУїдкЫЎЦНУцEДІЃЌВтЕУФГНЈжўЮяABЕФЖЅЖЫAЕФбіНЧЮЊ42ЁуЃЌЯђе§ЧАЗНЯђзп37УзЕНДяЕуDДІЃЌдйЭљаБЦТCDЩЯзп30УзЕНДяЕуCДІЃЌВтЕУНЈжўЮяABЕФЖЅЖЫAЕФбіНЧЮЊ63.5ЁуЃЌвбжЊаБЦТCDЕФЦТЖШЮЊiЃН1ЃК0.75ЃЌНЈжўЮяABДЙжБгкЦНЬЈBCЃЌЦНЬЈBCгыЫЎЦНУцDEЦНааЃЌЕуAЁЂBЁЂCЁЂDЁЂEОљдкЭЌвЛЦНУцФкЃЌдђНЈжўЮяABЕФИпЖШдМЮЊЃЈЁЁЁЁЃЉЃЈОЋШЗЕН0.1УзЃЌВЮПМЪ§ОнЃКsin42ЁуЁж0.67ЃЌcos42ЁуЁж0.74ЃЌtan42ЁуЁж0.90ЃЌsin63.5ЁуЁж0.90ЃЌcos63.5ЁуЁж0.45ЃЌtan63.5ЁуЁж2.0ЃЉ
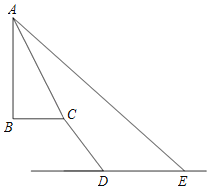
A.42.4УзB.46.4УзC.48.5УзD.50.8Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЫљЪОЃЌ![]() ЮЊОиаЮ
ЮЊОиаЮ![]() ЕФБп
ЕФБп![]() ЩЯвЛЕуЃЌЖЏЕу
ЩЯвЛЕуЃЌЖЏЕу![]() ,
,![]() ЭЌЪБДгЕу
ЭЌЪБДгЕу![]() ГіЗЂЃЌЕу
ГіЗЂЃЌЕу![]() биелЯп
биелЯп![]() дЫЖЏЕНЕу
дЫЖЏЕНЕу![]() ЪБЭЃжЙЃЌЕу
ЪБЭЃжЙЃЌЕу![]() би
би![]() дЫЖЏЕНЕу
дЫЖЏЕНЕу![]() ЪБЭЃжЙЃЌЫќУЧдЫЖЏЕФЫйЖШЖМЪЧ
ЪБЭЃжЙЃЌЫќУЧдЫЖЏЕФЫйЖШЖМЪЧ![]() УыЃЌЩш
УыЃЌЩш![]() ЁЂ
ЁЂ![]() ЭЌЪБГіЗЂ
ЭЌЪБГіЗЂ![]() УыЪБЃЌ
УыЪБЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() .вбжЊ
.вбжЊ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМЃЈ2ЃЉЃЈЧњЯп
ЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМЃЈ2ЃЉЃЈЧњЯп![]() ЮЊХзЮяЯпЕФвЛВПЗжЃЉдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
ЮЊХзЮяЯпЕФвЛВПЗжЃЉдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
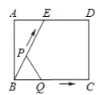
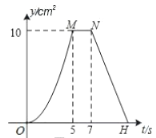
ЭМЃЈ1ЃЉ ЭМЃЈ2ЃЉ
A.![]() B.ЕБ
B.ЕБ![]() ЪЧЕШБпШ§НЧаЮЪБЃЌ
ЪЧЕШБпШ§НЧаЮЪБЃЌ![]() Уы
Уы
C.ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() УыD.ЕБ
УыD.ЕБ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЪЧ
ЕФжЕЪЧ![]() ЛђУы
ЛђУы![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() КЭ
КЭ![]() ЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() гы
гы![]() ЕФаББп
ЕФаББп![]() ЕФжаЕужиКЯЃЌНЋ
ЕФжаЕужиКЯЃЌНЋ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌа§зЊЙ§ГЬжаЃЌЯпЖЮ
а§зЊЃЌа§зЊЙ§ГЬжаЃЌЯпЖЮ![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЩфЯп
ЃЌЩфЯп![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌгыЩфЯп
ЃЌгыЩфЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() .
.
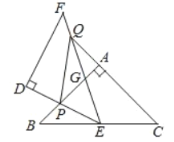
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЦНЗж
ЦНЗж![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУХфЗНЗЈНтЯТСаЗНГЬЃЌЦфжагІдкЗНГЬзѓгвСНБпЭЌЪБМгЩЯ4ЕФЪЧЃЈЁЁЁЁЃЉ
A. x2Љ2xЃН5 B. x2+4xЃН5 C. 2x2Љ4xЃН5 D. 4x2+4xЃН5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌABЃМADЃЌЁЯD=30ЁуЃЌCD=4ЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуEЃЌдђвѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ
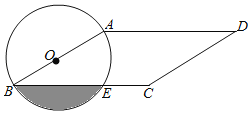
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com