
【题目】如图(1)所示,![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,动点
上一点,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,它们运动的速度都是
时停止,它们运动的速度都是![]() 秒,设
秒,设![]() 、
、![]() 同时出发
同时出发![]() 秒时,
秒时,![]() 的面积为
的面积为![]() .已知
.已知![]() 与
与![]() 的函数关系图象如图(2)(曲线
的函数关系图象如图(2)(曲线![]() 为抛物线的一部分)则下列结论正确的是( )
为抛物线的一部分)则下列结论正确的是( )
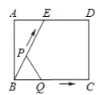
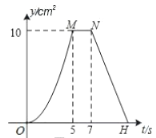
图(1) 图(2)
A.![]() B.当
B.当![]() 是等边三角形时,
是等边三角形时,![]() 秒
秒
C.当![]() 时,
时,![]() 秒D.当
秒D.当![]() 的面积为
的面积为![]() 时,
时,![]() 的值是
的值是![]() 或秒
或秒![]()
【答案】D
【解析】
先根据图象信息求出AB、BE、BE、AE、ED,
A、直接求出比,
B、先判断出∠EBC≠60°,从而得出点P可能在ED上时,△PBQ是等边三角形,但必须是AD的中点,而AE>ED,所以点P不可能到AD中点的位置,故△PBQ不可能是等边三角形;
C、利用相似三角形性质列出方程解决,分两种情况讨论计算即可,
D、分点P在BE上和点P在CD上两种情况计算即可.
由图象可知,AD=BC=BE=5,CD=AB=4,AE=3,DE=2,
A、∴AB:AD=5:4,故A错误,
B、∵tan∠ABE=![]() ,
,
∴∠ABE≠30°
∴∠PBQ≠60°,
∴点P在ED时,有可能△PBQ是等边三角形,
∵BE=BC,
∴点P到点E时,点Q到点C,
∴点P在线段AD中点时,有可能△PBQ是等边三角形,
∵AE>DE,
∴点P不可能到AD的中点,
∴△PBQ不可能是等边三角形,故B错误,
C、∵△ABE∽△QBP,
∴点E只有在CD上,且满足![]() ,
,
∴![]() ,
,
∴CP=![]() .
.
∴t=(BE+ED+DQ)÷1=5+2+(4![]() )=
)=![]() .
.
故C错误,
D、①如图(1)
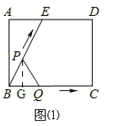
在Rt△ABE中,AB=4,BE=5
sin∠AEB=![]() ,
,
∴sin∠CBE=![]()
∵BP=t,
∴PG=BPsin∠CBE=![]() t,
t,
∴S△BPQ=![]() BQ×PG=
BQ×PG=![]() ×t×
×t×![]() t=
t=![]() t2=4,
t2=4,
∴t=![]() (舍)或t=
(舍)或t=![]() ,
,
②当点P在CD上时,
S△BPQ=![]() ×BC×PC=
×BC×PC=![]() ×5×(5+2+4t)=
×5×(5+2+4t)=![]() ×(11t)=4,
×(11t)=4,
∴t=![]() ,
,
∴当△BPQ的面积为4cm2时,t的值是![]() 或
或![]() 秒,故D正确,
秒,故D正确,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料.
(1)设计一种砌法,使矩形花园的面积为300m2.
(2)当BC为何值时,矩形ABCD的面积有最大值?并求出最大值.
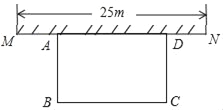
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:今有甲种袋子中装有黄金9枚(每枚黄金重量相同),乙种袋子中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲种袋子比乙种袋子轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,则可建立方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
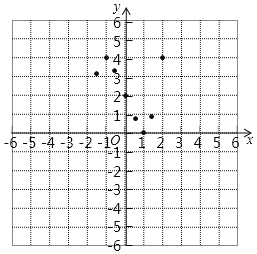
【题目】在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时 y=0.
(1)根据已知条件可知这个函数的表达式 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 在第一象限内交于
在第一象限内交于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() .
.

(1)![]() __________,
__________,![]() ____________________,
____________________,![]() ____________________.
____________________.
(2)直接写出不等式![]() 的解集;
的解集;
(3)设点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 是
是![]() 轴上一点,求
轴上一点,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
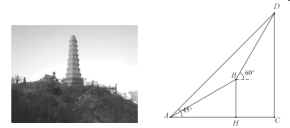
【题目】如图,为了测量山脚到塔顶的高度(即![]() 的长),某同学在山脚
的长),某同学在山脚![]() 处用测角仪测得塔顶
处用测角仪测得塔顶![]() 的仰角为
的仰角为![]() ,再沿坡度为
,再沿坡度为![]() 的小山坡前进400米到达点
的小山坡前进400米到达点![]() ,在
,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .
.
(1)求坡面![]() 的铅垂高度(即
的铅垂高度(即![]() 的长);
的长);
(2)求![]() 的长.(结果保留根号,测角仪的高度忽略不计).
的长.(结果保留根号,测角仪的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
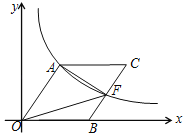
【题目】如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,点A的横纵坐标之比为3:4,反比例函数y=![]() (k>0)在第一象限内的图象经过点A,且与BC交于点F.
(k>0)在第一象限内的图象经过点A,且与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)∠A=∠GEF;(2)△BDF≌FEC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com