
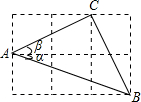
 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”) 分析 根据正切的概念和正方形网格图求出tanα和tanβ,根据等腰直角三角形的性质和tan45°的值求出tan(α+β),比较即可.
解答 解:由正方形网格图可知,tanα=$\frac{1}{3}$,tanβ=$\frac{1}{2}$,
则tanα+tanβ=$\frac{1}{2}$+$\frac{1}{3}$=$\frac{5}{6}$,
∵AC=BC,∠ACB=90°,
∴α+β=45°,
∴tan(α+β)=1,
∴tan(α+β)>tanα+tanβ,
故答案为:>.
点评 本题考查的是特殊角的三角函数值、锐角三角函数的定义以及等腰直角三角形的性质,熟记特殊角的三角函数值、正确理解锐角三角函数的定义是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
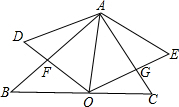 如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
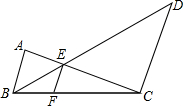 如图,AB∥EF∥DC,AB=20,CD=80,
如图,AB∥EF∥DC,AB=20,CD=80,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com