
若|b﹣1|+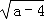 =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
=0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
科目:初中数学 来源: 题型:
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写 出一个代数恒等式是( )
出一个代数恒等式是( )

A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
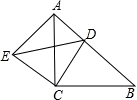
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
(1)求证:△ACE≌△BCD;
 (2)求证:△ADE是直角三角形;
(2)求证:△ADE是直角三角形;
(3)已知△ADE的面积为30cm2,DE=13cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
王刚同学在解关于x的方程x2﹣3x+c=0时,误将﹣3x看作+3x,结果解得x1=1,x2=﹣4,则原方程的解为( )
A.x1=﹣1,x2=﹣4 B.x1=1,x2=4 C.x1=﹣1,x2=4 D.x1=2,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
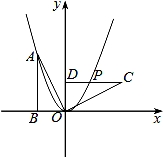
如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 .
1
查看答案和解析>>
科目:初中数学 来源: 题型:
.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若AB=2,∠P=30°,求AP的长(结果保留根号);
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com