
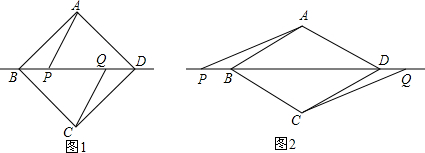
分析 (1)根据菱形的性质证明△ABP≌CDQ即可;
(2)证明菱形ABCD为正方形,得到BD=$\sqrt{2}$BA,得到答案;
(3)连接AC交BD于点H,证明BH=$\frac{\sqrt{3}}{2}$BA,又BP=DQ,得到答案.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
∴∠ABP=∠CDQ,
∵AP∥CQ,
∴∠APD=∠CQB,
∴∠APB=∠CQD,
在△ABP和CDQ中,
$\left\{\begin{array}{l}{∠APB=∠CQD}\\{∠ABP=∠CDQ}\\{AB=CD}\end{array}\right.$,
∴△ABP≌CDQ,
∴BP=DQ.
(2)∵∠ABC=90°,
∴菱形ABCD为正方形,
∴∠ABD=45°,∠BAD=90°,
∴在RT△ABD中,BD=$\frac{BA}{cos45°}$=$\sqrt{2}$BA,
由(1)得 BP=DQ,
∴BP+BQ=DQ+BQ=BD,
∴BP+BQ=$\sqrt{2}$BA.
(3)BP、BQ、BA之间的数量关系BQ-BP=$\sqrt{3}$BA,
理由如下:连接AC交BD于点H,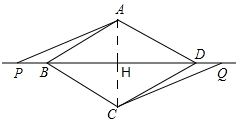
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABH=30°,∠AHB=90°,BD=2BH,
∴BH=AB•cos∠ABH=$\frac{\sqrt{3}}{2}$BA,
由(1)得,BP=DQ,
∴BQ-BP=BQ-DQ=BD=$\sqrt{3}$BA.
点评 本题考查的是菱形的性质,掌握菱形的四条边相等、对角线互相垂直和锐角三角函数的概念是解题的关键,注意确定三角形的性质和判定的灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
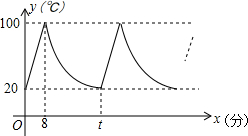 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
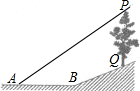 已知:如图,斜坡BQ坡度i=5:12(即为QC与BC的长度之比),在斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A,B,P,Q在同一平面上,PQ⊥AB于点C.求香樟树PQ的高度.
已知:如图,斜坡BQ坡度i=5:12(即为QC与BC的长度之比),在斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A,B,P,Q在同一平面上,PQ⊥AB于点C.求香樟树PQ的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com