
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.

(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
【答案】(1)证明见解析(2)证明见解析(3)2
【解析】
感知:先利用矩形性质得: ∠D=∠C=90°,再利用同角的余角相等得: ∠DAE=∠FEC,根据已知边的长度计算出AD=CE=3,则由ASA证得: △ADE≌△ECF;
探究:利用两角相等证明△PDE∽△ECF;
应用:作辅助线,构建如图②一样的相似三角形,利用探究得: △PDE∽△EGF,则![]() ,所以
,所以![]() ,再利用△PEF的面积是3,列式可得:PE·EF=6,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
,再利用△PEF的面积是3,列式可得:PE·EF=6,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
(1)证明:感知:如图①,∵四边形ABCD为矩形,
∴∠D=∠C=90°,
∴∠DAE+∠DEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠DEA+∠FEC=90°,
∴∠DAE=∠FEC,
∵DE=1,CD=4,
∴CE=3,
∵AD=3,
∴AD=CE,
∴△ADE≌△ECF(ASA)
(2)探究:如图②,∵四边形ABCD为矩形,
∴∠D=∠C=90°,
∴∠DPE+∠DEP=90°,
∵EF⊥PE,
∴∠PEF=90°,
∴∠DEP+∠FEC=90°,
∴∠DPE=∠FEC,
∴△PDE∽△ECF
(3)应用:解:如图③,过F作FG⊥DC于G,
∵四边形ABCD为矩形,
∴AB∥CD,
∴FG=BC=3,
∵PE⊥EF,
∴S△PEF=![]() PEEF=3,
PEEF=3,
∴PEEF=6,
同理得:△PDE∽△EGF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EF=3PE,
∴3PE2=6,
∴PE=±![]() ,
,
∵PE>0,
∴PE=![]() ,
,
在Rt△PDE中,由勾股定理得:PD=![]() =1,
=1,
∴AP=AD﹣PD=3﹣1=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,E、F分别是正方形AD、CD边上的点,且∠EBF=45°,对角线AC交BE,BF于M,N,对于以下结论,正确的是( )①AE+CF=FE②△ABE≌△BCF③AM2+CN2=MN2④△EFD的周长等于2AB

A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件.求:
(1)若商场每件衬衫降价4元,则商场每天可盈利多少元?
(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(3)要使商场平均每天盈利1600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
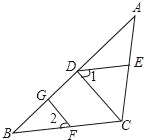
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com