Question

1．如图1，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴与G，连OB、OC．
（1）判断△AOG的形状，并予以证明；
（2）若点B、C关于y轴对称，求证：?AG=GB；?AO⊥OB．
（3）在（2）的条件下，如图2，点M为OA上一点，且∠ACM=45°，连接CB交y轴于P点，求证：OB=OM．

Answer 1

分析 （1）利用已知条件可证明∠GOA=∠GAO，由等腰三角形的判定可得AG=OG，所以△AOG是等腰三角形；
（2）由已知可得BK=KC，因为AC∥y轴，可得GA=GB；根据等腰三角形的性质得出∠GOB=∠GBO，∠AOG=∠OAG，所以∠AOG+∠BOG=∠OAG+∠OBG，即∠AOB=∠OAG+∠OBG，即可求得∠AOB=90°；
（3）先证得BM是∠ABC的平分线，设∠OBC=x，则x+∠POB=90°，而∠POA+∠POB=∠AOB=90°，求得x=∠POA，进一步证得x=∠GAM．根据∠OMB=∠GAM+∠ABM=x+∠ABM=x+∠PBM=∠MBO，即可证得结论．

解答 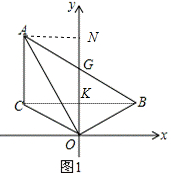解：（1）等腰三角形，
∵AC∥y轴，
∴∠OAC=∠AOG，
∵∠OAC=∠OAG，
∴∠AOG=∠OAG，
∴AG=OG，
∴△AOG是等腰三角形；
（2）如图1，设BC交y轴于K，
∵点B、C关于y轴对称，
∴CK=BK，
∵AC∥y轴，
∴AG=BG，
∵AG=OG，
∴OG=BG，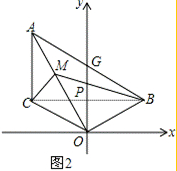
∴∠GOB=∠GBO，
∵∠AOG=∠OAG，
∴∠AOG+∠BOG=∠OAG+∠OBG，即∠AOB=∠OAG+∠OBG，
∴∠AOB=90°
∴AO⊥BO．
（3）如图2，∵∠ACM=45°，∠ACB=90°，
∴CM是∠ACB的平分线，
∵AM是∠BAC的平分线，
∴BM平分∠ABC，
设∠OBC=x，则x+∠POB=90°，而∠POA+∠POB=∠AOB=90°，
∴x=∠POA．
∵∠AOG=∠OAG，
∴x=∠GAM．
∴∠OMB=∠GAM+∠ABM
=x+∠ABM
=x+∠PBM
=∠MBO．
∴OB=OM．

点评 本题考查了角平分线的性质、轴对称的性质、等腰三角形的判定和性质、三角形的内角和定理，题目的综合性强，解题的关键是正确添加辅助线．