
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上一动点(不含端点),
边上一动点(不含端点),![]() 于
于![]() ,与直线
,与直线![]() 交于
交于![]() .
.
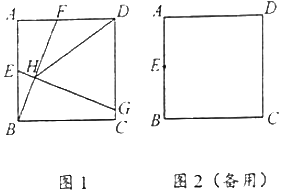
![]() 求证:
求证:![]() .
.
![]() 若
若![]() 试写出
试写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
![]() 求
求![]() 的最小值.
的最小值.
科目:初中数学 来源: 题型:
【题目】2020年3月24日,工信部发布《关于推动![]() 加快发展的通知》,全力推进
加快发展的通知》,全力推进![]() 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向
网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向![]() 迁移,推动“
迁移,推动“![]() 医疗健康”创新发展,实施“
医疗健康”创新发展,实施“![]() 工业互联网”512工程,促进“
工业互联网”512工程,促进“![]() 车联网”协同发展,构建
车联网”协同发展,构建![]() 应用生态系统.现“
应用生态系统.现“![]() 网络”已成为一个热门词汇,某校为了解九年级学生对“
网络”已成为一个热门词汇,某校为了解九年级学生对“![]() 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
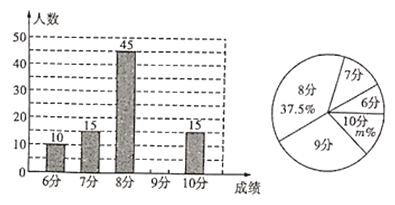
(1)请补全条形统计图,扇形统计图中![]() __;
__;
(2)所调查学生成绩的众数是_ ____分,平均数是_ 分;
(3)若该校九年级学生有![]() 人,请估计得分不少于
人,请估计得分不少于![]() 分的有多少人?
分的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
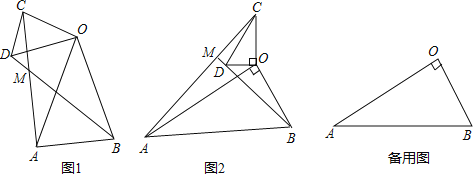
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是边
是边![]() 上的一个动点,过点
上的一个动点,过点![]() 作射线
作射线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,连接
,连接![]() .设
.设![]() ,
,![]() .小石根据学习函数的经验,对函数
.小石根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
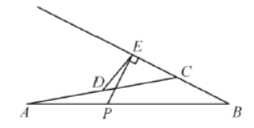
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如表:
的几组值,如表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(说明:补全表格时相关数据保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:点![]() 是
是![]() 边的中点时,
边的中点时,![]() 的长度约为_______
的长度约为_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于![]() ,超过
,超过![]() 时,所有这种水果的批发单价均为3元
时,所有这种水果的批发单价均为3元![]() .图中折线表示批发单价
.图中折线表示批发单价![]() (元
(元![]() )与质量
)与质量![]() 的函数关系.
的函数关系.
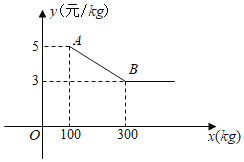
(1)求图中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)小李用800元一次可以批发这种水果的质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

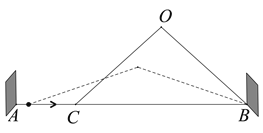
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早上匀速骑车去上学,出发几分钟后,爸爸发现小明的作业本丢在家里,赶紧匀速骑车去追.爸爸刚出发![]() 时,小明也发现作业本丢在家里,立刻按原路原速返回,
时,小明也发现作业本丢在家里,立刻按原路原速返回, ![]() 后遇到爸爸,爸爸把作业本交给小明后立刻按原路原速返回家,小明继续按原速骑车赶往学校.小明和爸爸相距的路程
后遇到爸爸,爸爸把作业本交给小明后立刻按原路原速返回家,小明继续按原速骑车赶往学校.小明和爸爸相距的路程![]() 与小明出发的时间
与小明出发的时间![]() 之间的关系如图所示(爸爸给小明作业本的时间忽略不计).下列说法中,错误的是( )
之间的关系如图所示(爸爸给小明作业本的时间忽略不计).下列说法中,错误的是( )
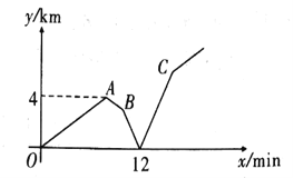
A.小明的骑车速度为![]() B.爸爸骑车的速度是小明的
B.爸爸骑车的速度是小明的![]() 倍
倍
C.点![]() 坐标为
坐标为![]() D.爸爸返回家时,小明共骑行了
D.爸爸返回家时,小明共骑行了![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与y轴交于点A(0,6),与x轴交于点B(﹣2,0),C(6,0).
(1)直接写出抛物线的解析式及其对称轴;
(2)如图2,连接AB,AC,设点P(m,n)是抛物线上位于第一象限内的一动点,且在对称轴右侧,过点P作PD⊥AC于点E,交x轴于点D,过点P作PG∥AB交AC于点F,交x轴于点G.设线段DG的长为d,求d与m的函数关系式,并注明m的取值范围;
(3)在(2)的条件下,若△PDG的面积为![]() ,
,
①求点P的坐标;
②设M为直线AP上一动点,连接OM交直线AC于点S,则点M在运动过程中,在抛物线上是否存在点R,使得△ARS为等腰直角三角形?若存在,请直接写出点M及其对应的点R的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com