
【题目】平行四边形ABCD中,经过对角线交点O的直线分别交AB、CD于点E、F.则图中全等的三角形共有( )

A. 4对 B. 5对 C. 6对 D. 8对
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某城市对居民生活用水按以下规定收取每月的水费:家庭月用水量如果不超过8吨,按每吨2.5元收费;如果超过8吨,未超过的部分仍按每吨2.5元收取,而超过部分则按每吨4元收取.
(1)设某家庭月用水量为x吨,水费为y元,请写出y与x之间的函数解析式,并在给定的平面直角坐标系中,画出该函数的图象;
(2)如果小明家按题中规定今年3月份应缴水费34元,那么今年3月份小明家用水多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并按要求解答.
(模型介绍)
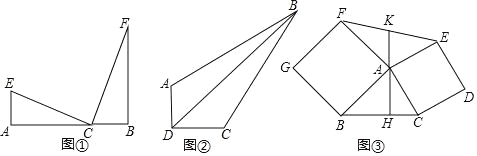
如图①,C是线段A、B上一点E、F在AB同侧,且∠A=∠B=∠ECF=90°,看上去像一个“K“,我们称图①为“K”型图.
(性质探究)
性质1:如图①,若EC=FC,△ACE≌△BFC
性质2:如图①,若EC≠FC,△ACE~△BFC且相似比不为1.
(模型应用)
应用1:如图②,在四边形ABCD中,∠ADC=90°,AD=1,CD=2,BC=2![]() ,AB=5.求BD.
,AB=5.求BD.
应用2:如图③,已知△ABC,分别以AB、AC为边向外作正方形ABGF、正方形ACDE,AH⊥BC,连接EF.交AH的反向延长线于点K,证明:K为EF中点.
(1)请你完成性质1的证明过程;
(2)请分别解答应用1,应用2提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)


查看答案和解析>>
科目:初中数学 来源: 题型:
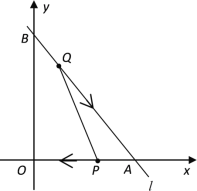
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,且
,且![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,动点
两点,动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒2个单位长度的速度向点
上以每秒2个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 移动,设点P、Q移动的时间为
移动,设点P、Q移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 是以PQ为底的等腰三角形?
是以PQ为底的等腰三角形?
(2)求出点P、Q的坐标;(用含![]() 的式子表达)
的式子表达)
(3)当![]() 为何值时,
为何值时,![]() 的面积是△ABO面积的
的面积是△ABO面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
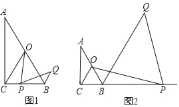
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中有一梯形ABCO,顶点C在x正半轴上,A、B两点在第一象限;且AB∥CO,AO=BC=2,AB=3,OC=5.点P在x轴上,从点(﹣2,0)出发,以每秒1个单位长度的速度沿x轴向正方向运动;同时,过点P作直线l,使直线l和x轴向正方向夹角为30°.设点P运动了t秒,直线l扫过梯形ABCO的面积为S扫.
(1)求A、B两点的坐标;
(2)当t=2秒时,求S扫的值;
(3)求S扫与t的函数关系式,并求出直线l扫过梯形ABCO面积的![]() 时点P的坐标.
时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com