
【题目】阅读下列材料,并按要求解答.
(模型介绍)
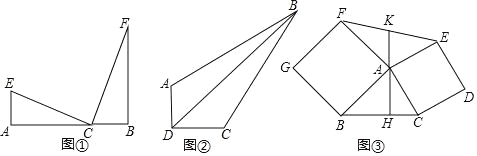
如图①,C是线段A、B上一点E、F在AB同侧,且∠A=∠B=∠ECF=90°,看上去像一个“K“,我们称图①为“K”型图.
(性质探究)
性质1:如图①,若EC=FC,△ACE≌△BFC
性质2:如图①,若EC≠FC,△ACE~△BFC且相似比不为1.
(模型应用)
应用1:如图②,在四边形ABCD中,∠ADC=90°,AD=1,CD=2,BC=2![]() ,AB=5.求BD.
,AB=5.求BD.
应用2:如图③,已知△ABC,分别以AB、AC为边向外作正方形ABGF、正方形ACDE,AH⊥BC,连接EF.交AH的反向延长线于点K,证明:K为EF中点.
(1)请你完成性质1的证明过程;
(2)请分别解答应用1,应用2提出的问题.
【答案】(1)证明见解析;(2)应用1: BD=4![]() ;应用2:证明见解析.
;应用2:证明见解析.
【解析】
(1)根据AAS即可证明;
(2)①应用1:如图2中,连接AC,作BH⊥DC交DC的延长线与H.首先证明符合“k模型”,利用性质2根据相似三角形的性质即可解决问题;
②应用2:如图③中,作FM⊥KH于M,EN⊥HN于N.由性质1可知:△ABH≌△FAM,△AHC≌△ENA,推出FM=AH,AH=EN,推出FM=EN,再证明△FKN≌△EKN即可解决问题.
(1)如图①中,
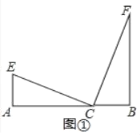
∵∠A=∠ECF=∠B=90°,
∴∠ACE+∠BCF=90°,∠BCF+∠F=90°,
∴∠ACE=∠F,∵EC=CF,
∴△ACE≌△BFC.
(2)①应用1:如图2中,连接AC,作BH⊥DC交DC的延长线与H.
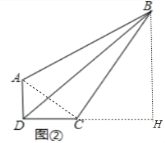
在Rt△ADC中,∵∠ADC=90°,AD=1,CD=2,
∴AC=![]() =
=![]() ,
,
∵AC2+BC2=5+20=25,AB2=52=25,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴∠ADC=∠ACB=∠CHB=90°,
∴符合“K”型图,
∴△ACD∽△CBH,
∴![]() ,
,
∴![]() ,
,
∵CH=2,BH=4,
∴DH=4,
在Rt△BDH中,BD=![]() =4
=4![]() .
.
应用2:如图③中,作FM⊥KH于M,EN⊥HN于N,
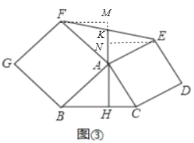
由性质1可知:△ABH≌△FAM,△AHC≌△ENA,
∴FM=AH,AH=EN,
∴FM=EN,
∵∠FKM=∠EKN,∠M=∠ENK=90°,
∴△FKN≌△EKN,
∴FK=KE,
∴K为EF中点.


科目:初中数学 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.
(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
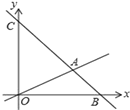
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是诸暨盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为________(用含a的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,经过对角线交点O的直线分别交AB、CD于点E、F.则图中全等的三角形共有( )

A. 4对 B. 5对 C. 6对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
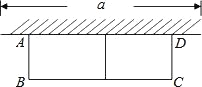
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com