
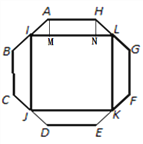
【题目】如图,正八边形ABCDEFGH的边长为a,I、J、K、L分别是各自所在边的中点,且四边形IJKL是正方形,则正方形IJKL的边长为________(用含a的代数式表示).

【答案】![]()
【解析】分析:过点A作AM⊥IL于点M,过点H作HN⊥IL与点N,可得四边形AMNH为矩形,根据正八边形的性质可得∠BAH=135°,由此可得∠BAM=45°,在等腰直角三角形AIM中,AI=![]() ,可求得AM=IM=
,可求得AM=IM=![]() ,同理求得HN=LN=
,同理求得HN=LN=![]() ,所以IL=IM+MN+LN=IM+AH+LN=
,所以IL=IM+MN+LN=IM+AH+LN=![]() +a+
+a+![]() =
=![]() .
.
详解:
过点A作AM⊥IL于点M,过点H作HN⊥IL与点N,可得四边形AMNH为矩形,
∵八边形ABCDEFGH为正八边形,
∴∠BAH=135°,
∵∠HAM=90°,
∴∠BAM=45°,
在等腰直角三角形AIM中,AI=![]()
∴AM=IM=![]() ;
;
同理求得HN=LN=![]() ,
,
∴IL=IM+MN+LN=IM+AH+LN=![]() +a+
+a+![]() =
=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小刘同学在一次课外活动中,用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .图①是小刘同学所做的一个数学探究:他将
.图①是小刘同学所做的一个数学探究:他将![]() 的直角边
的直角边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() 、
、![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).
重合).
(1)在![]() 沿
沿![]() 方向移动的过程中,小刘发现:
方向移动的过程中,小刘发现:![]() 、
、![]() 两点间的距离逐渐 ;连接
两点间的距离逐渐 ;连接![]() 后,
后,![]() 的度数逐渐 .(填“不变”、“变大”或“变小”);
的度数逐渐 .(填“不变”、“变大”或“变小”);
(2)小刘同学经过进一步地研究,编制了如下问题:
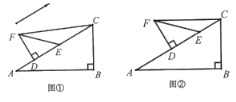
问题①:如图②,当![]() 、
、![]() 的连线与
的连线与![]() 平行时,求平移距离
平行时,求平移距离![]() 的长;
的长;
问题②:如图③,在![]() 的移动过程中,
的移动过程中,![]() 的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.
的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD.(S表示面积)
实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1,得到矩形A1B1C1D1.
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+![]() .
.
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF=![]() ,求EG的长.
,求EG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,正方形ABCD的面积等于100,l2与l3的距离为( )

A. 8B. 10C. 9D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数![]() 的图像经过点E,则k的值是 ( )
的图像经过点E,则k的值是 ( )

(A)33 (B)34 (C)35 (D)36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生![]() 其中甲校学生多于乙校学生,且甲校学生不足90名
其中甲校学生多于乙校学生,且甲校学生不足90名![]() ,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装,一共应付5000元
(1)甲、乙两校各有多少名学生准备参加汇演?
(2)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】简答题:
(1)当![]() 为何值时,关于
为何值时,关于![]() 的方程
的方程![]() 是一元二次方程?
是一元二次方程?
(2)已知关于![]() 的一元二次方程
的一元二次方程![]() 有一个根是0,求
有一个根是0,求![]() 的值.
的值.
(3)在第(2)题中,如果要使已知方程有一个根是l,那么m应该等于什么数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B测得仰角为60°,已知AB=20米,点C和直线AB在同一铅垂平面上,求气球离地面的高度.(结果精确到0.1米)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com