
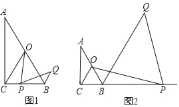
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).
【答案】(1) BQ=CP.理由见解析;(2) 成立:PC=BQ, 理由见解析.
【解析】
(1)由∠ACB=90°,∠A=30°得到∠ABC=60°,根据直角三角形斜边上中线性质得到OB=OC,则可判断△OCB、△CPH为等边三角形,作辅助线PH∥AB交CO于H,证明△POH≌△QPB全等可得PH=QB= PC;
(2)与(1)的证明方法同样得到△POH≌△QPB,可得PH=QB= PC。
解:(1)结论:BQ=CP.
理由:如图1中,作PH∥AB交CO于H.

在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,
∴CO=AO=BO,∠CBO=60°,
∴△CBO是等边三角形,
∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,
∴∠CHP=∠CPH=60°,
∴△CPH是等边三角形,
∴PC=PH=CH,
∴OH=PB,
∵∠OPB=∠OPQ+∠QPB=∠OCB+∠COP,
∵∠OPQ=∠OCP=60°,
∴∠POH=∠QPB,
∵在△POH与△QPB中
![]() ,
,
∴△POH≌△QPB(SAS),
∴PH=QB,
∴PC=BQ.
(2)成立:PC=BQ.

理由:作PH∥AB交CO的延长线于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,
∴CO=AO=BO,∠CBO=60°,
∴△CBO是等边三角形,
∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,
∴∠CHP=∠CPH=60°,
∴△CPH是等边三角形,
∴PC=PH=CH,
∴OH=PB,
∵∠POH=60°+∠CPO,∠QPO=60°+∠CPQ,
∴∠POH=∠QPB,
∵在△POH与△QPB中
![]() ,
,
∴△POH≌△QPB(SAS),
∴PH=QB,
∴PC=BQ.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】草莓是诸暨盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,经过对角线交点O的直线分别交AB、CD于点E、F.则图中全等的三角形共有( )

A. 4对 B. 5对 C. 6对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图将小球从斜坡的O点抛出,小球的抛出路线可以用二次函数y=ax2+bx刻画,顶点坐标为(4,8),斜坡可以用y=![]() x刻画.
x刻画.
(1)求二次函数解析式;
(2)若小球的落点是A,求点A的坐标;
(3)求小球飞行过程中离坡面的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点,![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0两根为x1,x2,x2+x1=﹣![]() ,x2.x1=
,x2.x1=![]() .如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为( )
.如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为( )
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
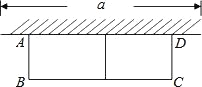
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
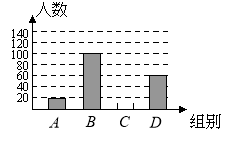
A组:![]() ;B组:
;B组:![]()
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
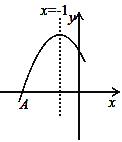
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
其中正确的结论是(填写代表正确结论的序号)__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com