
【题目】已知一元二次方程ax2+bx+c=0两根为x1,x2,x2+x1=﹣![]() ,x2.x1=
,x2.x1=![]() .如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为( )
.如果抛物线y=ax2+bx+c经过点(1,2),若abc=4,且a≥b≥c,则|a|+|b|+|c|的最小值为( )
A. 5 B. 6 C. 7 D. 8
【答案】B
【解析】
易知:b+c=2-a,bc=![]() ,可将b、c看做是一元二次方程x2-(2-a)x+
,可将b、c看做是一元二次方程x2-(2-a)x+![]() =0的两实根,那么可根据△≥0,求得a的大致取值范围为a≥4.由于abc=4>0,且a≥b≥c,则说明:①a、b、c均大于0,由于a≥4,如果三数均为正数,显然a+b+c>4≠2,因此不合题意;
=0的两实根,那么可根据△≥0,求得a的大致取值范围为a≥4.由于abc=4>0,且a≥b≥c,则说明:①a、b、c均大于0,由于a≥4,如果三数均为正数,显然a+b+c>4≠2,因此不合题意;
②a正,b、c为负,那么此时|a|+|b|+|c|=a-(b+c)=a-(2-a)=2a-2,根据得出的a的取值范围,即可求出|a|+|b|+|c|的最小值.
∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾,
∴a>0;
∵b+c=2-a,bc=![]() ,
,
∴b,c是一元二次方程x2-(2-a)x+![]() =0的两实根,
=0的两实根,
∴△=(2-a)2-4×![]() ≥0,
≥0,
∴a3-4a2+4a-16≥0,即(a2+4)(a-4)≥0,故a≥4,
∵abc>0,
∴a,b,c为全大于0或一正二负;①若a,b,c均大于0,
∵a≥4,与a+b+c=2矛盾;
②若a,b,c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,
∵a≥4,
故2a-2≥6,
当a=4,b=c=-1时,满足题设条件且使不等式等号成立,
故|a|+|b|+|c|的最小值为6.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是对角线,
是对角线,![]() 交
交![]() 延长线于
延长线于![]() .若四边形
.若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 是( )
是( )
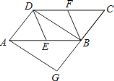
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:

(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列例题的解答过程:解方程:3(x﹣2)2+7(x﹣2)+4=0.
解:设 x﹣2=y,则原方程化为:3y2+7y+4=0.
∵a=3,b=7,c=4,∴b2﹣4ac=72﹣4×3×4=1.
∴y=![]() =
=![]() .∴y1=﹣1,y2=﹣
.∴y1=﹣1,y2=﹣![]() .
.
当 y=﹣1 时,x﹣2=﹣1,∴x=1;
当 y=﹣![]() 时,x﹣2=﹣
时,x﹣2=﹣![]() ,∴x=
,∴x=![]() .
.
∴原方程的解为:x1=1,x2=![]() .
.
(1)请仿照上面的例题解一元二次方程:2(x﹣3)2﹣5(x﹣3)﹣7=0;
(2)若(a2+b2)(a2+b2﹣2)=3,求代数式 a2+b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,点
,点![]() 为斜边
为斜边![]() 的中点,
的中点,![]() 是直角三角形,
是直角三角形,![]() .
.![]() 保持不动,将
保持不动,将![]() 沿射线
沿射线![]() 向左平移,平移过程中点
向左平移,平移过程中点![]() 始终在射线
始终在射线![]() 上,且保持
上,且保持![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
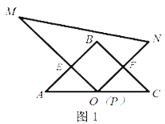
(2)如图2,当点![]() 在线段
在线段![]() 上时,猜想
上时,猜想![]() 与
与![]() 有怎样的数量关系与位置关系,并对你的猜想结果给予证明;
有怎样的数量关系与位置关系,并对你的猜想结果给予证明;
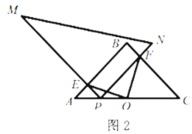
(3)如图3,当点![]() 在
在![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,则
,则![]() 的长为__________.
的长为__________.
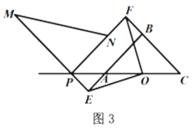
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
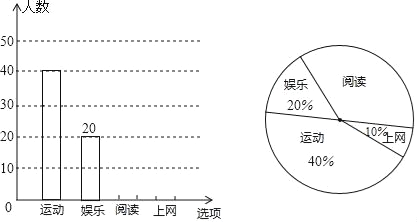
(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=4,∠A=60°,若边AC的垂直平分线DE交AB于点D,连接CD,则△BDC的周长为( )
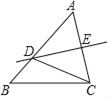
A. 8 B. 9 C. 5+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AB 是⊙O 的直径,点 C、D 在⊙O 上,过 D 点作 PF∥AC交⊙O 于 F,交 AB 于点 E,∠BPF=∠ADC
(1)求证:AEEB=DEEF.
(2)求证:BP 是⊙O 的切线:
(3)当的半径为![]() ,AC=2,BE=1 时,求 BP 的长,
,AC=2,BE=1 时,求 BP 的长,

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com