
����Ŀ����ͼ����ֱ������ϵxOy����һ����ABCO������C��x�������ϣ�A��B�����ڵ�һ���ޣ���AB��CO��AO��BC��2��AB��3��OC��5����P��x���ϣ��ӵ㣨��2��0����������ÿ��1����λ���ȵ��ٶ���x�����������˶���ͬʱ������P��ֱ��l��ʹֱ��l��x����������н�Ϊ30�㣮���P�˶���t�룬ֱ��lɨ������ABCO�����ΪSɨ��
��1����A��B��������ꣻ
��2����t��2��ʱ����Sɨ��ֵ��
��3����Sɨ��t�ĺ�����ϵʽ�������ֱ��lɨ������ABCO�����![]() ʱ��P�����꣮
ʱ��P�����꣮

���𰸡���1����1��![]() ������4��
������4��![]() ������2��
������2��![]() ����3��
����3��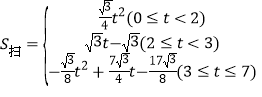 ��P��������5��2
��P��������5��2![]() ��0����
��0����
��������
��1�����IJ��һ�����A�ĺ���������A��B��x��Ĵ������ڹ�����ֱ���������и���OA�ij������IJ���������εĸ�A��������꣮�ó�A�����������ƽ��3����λ����B���������
��2����t��2ʱ��P��O�����غ��������ֱ��l��AB�Ľ���ΪD����ôAD��2����AD���ϵĸ߾���A������������ɴ˿������ADO�������ֱ��lɨ���������
��3������Ҫ�������������������
����P��ԭ�����������0��t��2ʱ���غϲ����Ǹ��������������ֱ��l��AO��AB�ֱ���E��F���ɸ��ݡ�AEF�ס�AOD�������Ʊ��������������ɵó�S��t�ĺ�����ϵʽ��
����P��O���Ҳࣨ������O�غϣ�����F����B�����ʱ������2��t��3ʱ��ɨ�������Ǹ��������ɸ������ε�������㷽�����ɵó�ֱ��lɨ�����ֵ������Ҳ���ܵó�S��t�ĺ�����ϵʽ��
����P����C����ࣨ������C���غϣ���F����B���Ҳࣨ������B���غϣ�������3��t��7ʱ��ɨ�������Ǹ����������������ABCO�������ȥ��MPC��������ó�S��t�ĺ�����ϵʽ��
��1����A��AD��OC��D����B��BE��OC��E����ADEB�Ǿ�����
��ADEB�Ǿ�������AD=BE=3��
��AO=BC�����AOD�ա�BCE����OD=CE=��OC��AB����2=1��
��AO=2����AD=![]() =
=![]() ����A��1��
����A��1��![]() ����
����
��OE=OD+DE=1+3=4��BE=AD=![]() ����B��4��
����B��4��![]() ����
����
��BC=2EC�����EBC=30�㣬���OCB=60�㣮
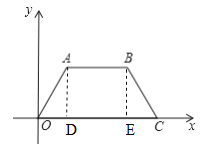
��2����t��2ʱ��P��O�����غ��������ֱ��l��AB�Ľ���ΪD����ôAD��2����AD���ϵĸ߾���A�������������Sɨ=![]() =
=![]() ��
��
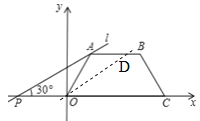
��3���������������������0��t��2ʱ����ͼ1����AEF�ס�AOD��![]() ����Sɨ
����Sɨ![]() t2��
t2��
����2��t��3ʱ����ͼ2��Sɨ��S��AOD+S��DOPF![]() ��t��2������Sɨ
��t��2������Sɨ![]() ��
��
����3��t��7ʱ����ͼ3����B��ֱ��EB��ֱ��l��OC��E��
�ߡ�BEC=30�㣬��OCB=60�㣬���CBE=90�㣬��EC=2BC=4����S��CEB=![]() ��CP=7��t��
��CP=7��t��
��MP��BE����![]() ����S��CPM��
����S��CPM��![]() ����Sɨ��4
����Sɨ��4![]() S��CPM��4
S��CPM��4![]() ����Sɨ
����Sɨ![]() t2
t2![]()
����������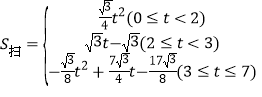 ��
��
��![]() t2
t2![]() ����t2��14t+41��0��t1��7��2
����t2��14t+41��0��t1��7��2![]() ��t2��7+2
��t2��7+2![]() 7���ᣩ����P������Ϊ��5��2
7���ᣩ����P������Ϊ��5��2![]() ��0����
��0����


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı���ABCD�У������Խ��߽���O��ֱ�߷ֱ�AB��CD�ڵ�E��F.��ͼ��ȫ�ȵ������ι��У� ��

A. 4�� B. 5�� C. 6�� D. 8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
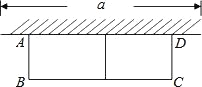
����Ŀ����ͼ���г�Ϊ 24m ����ʣ���һ������ǽ��ǽ�������ó��� a Ϊ 10m��Χ���м����һ����ʵij����λ��ԣ��軨�ԵĿ� AB Ϊ xm�����Ϊ Sm2��
��1�� �� S �� x �ĺ�����ϵʽ�� x ֵ��ȡֵ��Χ��
��2�� ҪΧ�����Ϊ 45m2 �Ļ��ԣ�AB �ij��Ƕ����ף�
��3�� �� AB �ij��Ƕ�����ʱ��Χ�ɵĻ��Ե�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ涨����Сѧ��ÿ����У�����ʱ�䲻����1Сʱ����Ϊ�ˣ�ij�о�����ÿ����У�����ʱ���Ƕ��������������������Ͻ����300������ѧ�������ݵ��������Ƴɵ�ͳ��ͼ�����֣���ͼ��ʾ�����з�������ǣ�
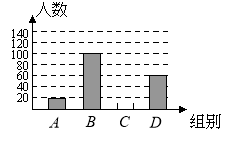
���飺![]() �����飺
�����飺![]()
���飺![]() ���飺
���飺![]()
�����������Ϣ����������⣺
��1���������������
��2�����ε������ݵ���λ���������ڣ�
��3������Ͻ��Լ��24 000������ѧ��������������д���ҹ涨�����ʱ�����Լ�ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
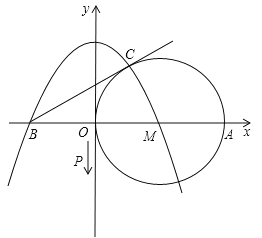
����Ŀ����ͼ����ƽ��ֱ������ϵ�����Ե�M��2��0��ΪԲ�ĵ���M��y��������ԭ��O������B����2��0������M���������е�ΪC��������![]() ������B�͵�M��
������B�͵�M��
��1�������������߽���ʽ��
��2�����C�����������жϵ�C�Ƿ��ڣ�1��������������
��3������P��ԭ��O��������y�Ḻ������ÿ��1����λ�����ٶ������˶������˶�t��ʱ�����Q������ʱ��BOQ����MCBȫ������t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+2��x���ཻ��A����1��0����B��4��0�����㣬��y���ཻ�ڵ�C��
��1���������ߵĽ���ʽ��
��2������ABC��AB�е�M��ת180�����õ���BAD��
�����D�����ꣻ
���ж��ı���ADBC����״����˵�����ɣ�
��3���ڸ������߶Գ������Ƿ���ڵ�P��ʹ��BMP���BAD���ƣ������ڣ��������������������P������ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�������н����У���ac��0����a+b+c��0����4a��2b+c��0����2a+b��0����4ac��b2��4a����a+b��0�У�������ȷ�ĸ���Ϊ�� ��
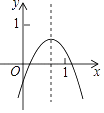
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
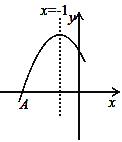
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1���������½��ۣ���abc��0 ��b2��4ac��0 ��4b+c��0 ����B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2������3��x��1ʱ��y��0��
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2������3��x��1ʱ��y��0��
������ȷ�Ľ����ǣ���д������ȷ���۵���ţ�__________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������OABC��ͼ���ã�OΪԭ�㣮����A����1��2������B����������![]() �����C�������ǣ�������
�����C�������ǣ�������

A. ��4��2�� B. ��2��4�� C. ��![]() ��3�� D. ��3��
��3�� D. ��3��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com