练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，P是反比例函数y=$\frac{6}{x}$图象上一点，PA⊥x轴于点A，则△POA的面积S△POA=3．

    分析 设出点P的坐标，△OAP的面积等于点P的横纵坐标的积的一半，把相关数值代入即可．

    解答 解：设点P的坐标为（x，y）．
    ∵P（x，y）在反比例函数y=$\frac{6}{x}$的图象上，
    ∴xy=6，
    ∴△OPM的面积S△POA=$\frac{1}{2}$xy=3，
    故答案为：3．

    点评 题考查了反比例函数比例系数k的几何意义：在反比例函数y=$\frac{k}{x}$图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．计算：$\frac{x}{x+1}-\frac{2x+6}{{x}^{2}-1}÷\frac{x+3}{x-1}$，并选一个合适的x代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

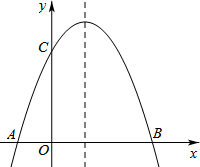    14．如图，已知抛物线y=ax2-2ax+3（a≠0）与x轴交于A、B两点，与y轴交于点C，且OB=3OA．
    （1）此抛物线的对称轴为直线x=1；并求出OA的长；
    （2）求此抛物线的解析式；
    （3）此二次函数x轴上方的图象上有一点E到A、B两点距离相等，求出△ABE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，直线a，b相交于点O，若∠1等于40°，则∠2等于（　　）
    A．140°B．120°C．60°D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

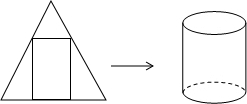    18．如图，在一个边长为4的等边三角形纸片中，截出一个面积最大的矩形，并用该矩形围成一个圆柱形无底纸筒，则纸筒的高为2或$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

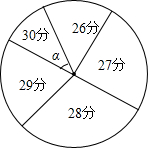    8．某校组织了九年级学生英语口语模拟测试，现从中随机抽取部分学生的口语模拟测试成绩统计如下．
    口语成绩（分）人数（人）百分比（%）
    26816
    2724
    2815
    29m
    305
    根据上面提供的信息，回答下列问题：
    （1）扇形统计图中的圆心角a=36°；
    （2）统计表中样本容量m=10；
    （3）已知该校九年级共有400名学生，如果口语成绩达28分以上（含28分）为优秀，请估计该校九年级学生口语成绩达到优秀的总人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

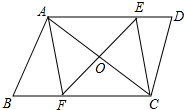    15．如图，平行四边形ABCD中，EF垂直平分AC，与边AD、BC分别相交于点E、F．则四边形AECF一定是（　　）
    A．正方形B．矩形C．菱形D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，四边形ABCO为正方形．
    （1）若点A坐标为（0，$\sqrt{10}$）
    ①求点B的坐标；
    ②如图2，点D为y轴上一点，连接BD，若点A到BD的距离为l，求点C到BD的距离；
    （2）如图3，连接正方形ABCO的对角线AC，OB交于点Q，点F为线段BC上一点，以OF为直角边向上构造等腰Rt△EOF，∠EOF=90°，EF交AC于P．若PQ=1，求CF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

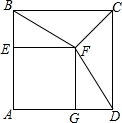    8．如图，正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上，连接BF、DF．
    （1）求证：BF=DF；
    （2）连接CF，请直接写出$\frac{CF}{BE}$的值为$\sqrt{2}$ （不必写出计算过程）．

    查看答案和解析>>

    同步练习册答案