练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简：÷（﹣），再从﹣2＜x＜3的范围内选取一个你最喜欢的值代入，求值．


    【考点】分式的化简求值．

    【专题】计算题．

    【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．

    【解答】解：原式=÷=•=，

    当x=2时，原式=4．

    【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

    A．∠3=∠4   B．∠1=∠2   C．∠D=∠DCE    D．∠D+∠ACD=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF．

    （1）求证：BE=DF；

    （2）连接AC交EF于点O，延长OC至点M，使OM=OA，连接EM，FM，判断四边形AEMF是什么特殊四边形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，三个正方形围成一个直角三角形，64，400分别为所在正方形的面积，则图中字母所代表的正方形面积是（　　）

    A．400+64     B．       C．400﹣64   D．4002﹣642

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商场同时购进甲、乙两种商品共200件，其进价和售价如下表，

    商品名称

    甲

    乙

    进价（元/件）

    80

    100

    售价（元/件）

    160

    240

    设其中甲种商品购进x件

    （1）若该商场购进这200件商品恰好用去17900元，求购进甲、乙两种商品各多少件？

    （2）若设该商场售完这200件商品的总利润为y元．

    ①求y与x的函数关系式；

    ②该商品计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？

    （3）实际进货时，生产厂家对甲种商品的出厂价下调a元（50＜a＜70）出售，且限定商场最多购进120件，若商场保持同种商品的售价不变，请你根据以上信息及（2）中的条件，设计出使该商场获得最大利润的进货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，由几个相同的小正方体搭成的一个几何体，它的左视图为（　　）

    A．  B．   C．  D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（　　）

    A．2  B．2  C．3       D．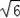

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E．求证：AD∥BC．

    查看答案和解析>>

    同步练习册答案