练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】△ABC在平面直角坐标系中的位置如图所示．

    （1）作△ABC关于原点O成中心对称的△A1B1C1 ．
    （2）请写出点B关于y轴对称的点B2的坐标 ． 若将点B2向下平移h单位，使其落在△A1B1C1内部（不包括边界），直接写出h的值（写出满足的一个即可）．

    【答案】
    （1）

    A1（2，-3），B1（1，-1），C1（0，-2）


    （2）（1,1）；3
    【解析】（1）画出三角形A1B1C1，关键是确定三点的坐标，根据关于原点成中心对称即可求得。
    （2）求得B2的坐标关键是关于y轴对称，横坐标变为原来的相反数，纵坐标不变。2h3.5,通过观察图像向下平移3各单位即可。
    【考点精析】掌握坐标与图形变化-平移是解答本题的根本，需要知道新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】襄阳农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数，得到如下数据：

    日期

    12月1日

    12月2日

    12月3日

    12月4日

    12月5日

    温差x（℃）

    10

    11

    13

    12

    8

    发芽数y（颗）

    23

    26

    32

    26

    16

    襄阳农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．
    （1）求选取的2组数据恰好是不相邻的2天数据的概率；
    （2）若选取的是12月1日与12月5日这两组数据，情根据12月2日至12月4日的数据，求y关于x的线性回归方程 = x+ ；
    （3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？ 注： = = ， = ﹣ ．

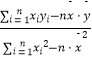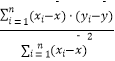    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图所示的几何体中，平面ADNM⊥平面ABCD，四边形ABCD是菱形，ADNM是矩形， ，AB=2，AM=1，E是AB的中点．
    （1）求证：平面DEM⊥平面ABM；
    （2）在线段AM上是否存在点P，使二面角P﹣EC﹣D的大小为 ？若存在，求出AP的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣2|+|2x+a|，a∈R． （Ⅰ）当a=1时，解不等式f（x）≥5；
    （Ⅱ）若存在x0满足f（x0）+|x0﹣2|＜3，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某蛋糕店每天制作生日蛋糕若干个，每个生日蛋糕的成本为50元，然后以每个100元的价格出售，如果当天卖不完，剩下的蛋糕作垃圾处理．现需决策此蛋糕店每天应该制作几个生日蛋糕，为此搜集并整理了100天生日蛋糕的日需求量（单位：个），得到如图3所示的柱状图，以100天记录的各需求量的频率作为每天各需求量发生的概率．若蛋糕店一天制作17个生日蛋糕．
    （1）求当天的利润y（单位：元）关于当天需求量n（单位：个，n∈N）的函数解析式；
    （2）求当天的利润不低于750元的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线 交x轴的正半轴于点A ， 点B（ ，a）在抛物线上，点C是抛物线对称轴上的一点，连接AB、BC ， 以AB、BC为邻边作□ABCD ， 记点C纵坐标为n ，

    （1）求a的值及点A的坐标；
    （2）当点D恰好落在抛物线上时，求n的值；
    （3） 记CD与抛物线的交点为E，连接AE，BE，当三角形AEB的面积为7时，n=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知与成正比例，且当时，.

    (1)写出与之间的函数表达式;

    (2)当时，求的值;

    (3)若y的取值范围为，求的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，∠C=90°，BC=3，D，E分别在AB、AC上，将△ADE沿DE翻折后，点A落在点A′处，若A′为CE的中点，则折痕DE的长为（ ）
    A.
    B.3
    C.2
    D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知下列命题：
    ①在Rt△ABC中，∠C=90°，若∠A＞∠B，则sin∠A＞sinB；
    ②四条线段a，b，c，d中，若=，则ad=bc；
    ③若a＞b，则a（m2+1）＞b（m2+1）；
    ④若|﹣x|=﹣x，则x≥0．
    其中原命题与逆命题均为真命题的是（　　）
    A.①②③
    B.①②④
    C.①③④
    D.②③④

    查看答案和解析>>

    同步练习册答案