
【题目】深圳市某校对初三综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分 100 分)两部分组成,其中测试成绩占 80%,平时成绩占 20%,并且当综合评价得分大于或
等于80 分时,该生综合评价为A 等.
(1)小明同学的测试成绩和平时成绩两项得分之和为185 分,而综合评价得分为91 分,则小明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70 分,他的综合评价得分有可能达到A 等吗?为什么?
(3)如果一个同学综合评价要达到A 等,他的测试成绩至少要多少分?
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)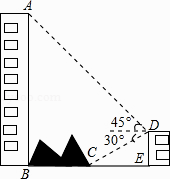
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD 中,AE 平分∠BAD,交BC 于E,DE⊥AE,下列结论:①DE平分∠ADC;②E 是BC 的中点;③AD=2CD;④四边形ADCE 的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x﹣6分别交x轴,y轴于A,B,M是反比例函数y=
x﹣6分别交x轴,y轴于A,B,M是反比例函数y= ![]() (x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=4
(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=4 ![]() ,则k的值为( )
,则k的值为( ) 
A.﹣3
B.﹣4
C.﹣5
D.﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
(1)若m=﹣3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE= ![]() S△ACD , 求点E的坐标;
S△ACD , 求点E的坐标;
(3)如图2,设F(﹣1,﹣4),FG⊥y于G,在线段OG上是否存在点P,使∠OBP=∠FPG?若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+b与反比例函数y= ![]() (x>0)的图象交于点A(m,3)和B(3,1).
(x>0)的图象交于点A(m,3)和B(3,1). 
(1)填空:一次函数的解析式为 , 反比例函数的解析式为;
(2)点P是线段AB上一点,过点P作PD⊥x轴于点D,连接OP,若△POD的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y= ![]() (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= ![]() .
. 
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com