
����Ŀ����ͼ��������A��B��C�����ʾ�����ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]()
(1)��![]() = ��
= �� ![]() = ��
= ��
(2)����P��A���������ÿ��10����λ���ٶ������������˶�������B��ͣ��Ƭ�̺�������ÿ��6����λ���ٶ������᷵�ص�A�㣬������6�룻���д�C��B������ʱ��B��C(������B��ͣ����ʱ��)������2����
����C���ʾ����![]() ��
��
�����˶�ʱ��Ϊ![]() �룬��
�룬��![]() Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
Ϊ��ֵʱ����P��A��B��C����ľ���֮��Ϊ23����λ��
���𰸡���1��a=��8��b=12����2��7����3��1.2��1.8��3��4.
�������������������1������ż�η��Լ�����ֵ�ķǸ��Լ������a��b��ֵ��
��2����AC=x��������AC�������˶���ʱΪ6-2=4���з�����⼴�ɣ�
��3����4��������з������ۼ��ɵý�.
�����������1����![]()
��a+8=0��b-12=0��
��ã�a=-8��b=12��
��2����AC=x����������ã�
![]() ��
��
���x=15��
c=��8+15=7��
��3���ٵ�P��A��B��AC���˶�ʱ����t��ʱ����P��A��B��C����ľ���֮��Ϊ23����λ����������ã�
-8+10t+7-10+12-10t=23
��ã�t=1.2
�ڵ�P��A��B��CB���˶�ʱ����t��ʱ����P��A��B��C����ľ���֮��Ϊ23����λ����������ã�
10t+10t-7+12-10t=23
��ã�t=1.8
ͬ���ɵã�t=3��t=4.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
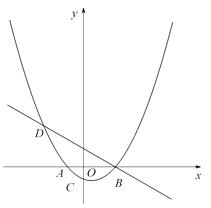
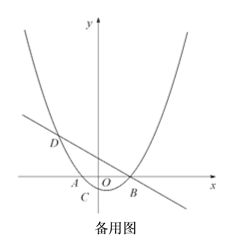
����Ŀ����ͼ����֪������![]() (aΪ��������a��0)��x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��
(aΪ��������a��0)��x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��![]() �������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
��1���������ߵĺ�������ʽ��
��2��PΪֱ��BD�·����������ϵ�һ�㣬����PD��PB, ����PBD��������ֵ��
��3����FΪ�߶�BD��һ��(�����˵�)������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͳ�ƣ��μӽ��������г��б�ҵ����ѧͳһ���Ե�ѧ��Լ36800�ˣ���������ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD�������Σ�M��AB�ӳ�����һ�㣮ֱ�����dzߵ�һ��ֱ�DZ߾�����D����ֱ�Ƕ���E��AB���ϻ�������E�����A��B�غϣ�����һֱ�DZ�����CBM��ƽ����BF�ཻ�ڵ�F��

��1����ͼ1������E��AB�ߵ��е�λ��ʱ��
��ͨ������DE��EF�ij��ȣ�����DE��EF�����������ϵ�� ��
�����ӵ�E��AD�ߵ��е�N������NE��BF�����������ϵ�� ����֤����IJ��룮
��2����ͼ2������E��AB���ϵ�����λ��ʱ�������ʱDE��EF��������������ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��3x��ͼ����y������ƽ��2����λ���Ⱥ�����ͼ���Ӧ�ĺ�����ϵʽΪ�� ��
A.y=��3x+2
B.y=��3x��2
C.y=��3��x+2��
D.y=��3��x��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com