
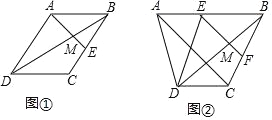
【题目】探究:如图①,在ABCD中,E为BC的中点,AE与BD相交于点M.求证:![]() .
.
应用:如图②,在四边形ABCD中,AB∥CD,AB=2CD,点E、F分别为AB、BC的中点,EF与BD相交于点M,连结AC.若ME=3,则AC的长为 .
【答案】证明见解析 AC=9
【解析】
(1)根据四边形ABCD是平行四边形,从而得到线段间的位置关系,利用三角形相似即可解答.
(2)根据点E、F分别为AB、BC的中点,求出四边形BCDE为平行四边形,再利用中位线即可解答.
探究:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EBM=∠ADM,∠BEM=∠DAM,
∴△EBM∽△ADM,
∴![]() =
=![]() .
.
∵点E为BC的中点,
∴EB=![]() BC=
BC=![]() AD,
AD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.
应用:解:∵AB∥CD,AB=2CD,点E为AB的中点,
∴BE=![]() AB=CD,
AB=CD,
∴四边形BCDE为平行四边形.
又∵点F为BC的中点,
∴![]() =
=![]() .
.
∵ME=3,
∴EF=ME+MF=3+![]() =
=![]() .
.
∵点E、F分别为AB、BC的中点,
∴EF为△BAC的中位线,
∴AC=2EF=9.
故答案为:9.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
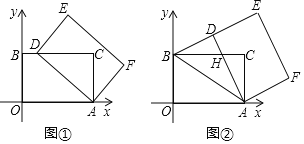
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
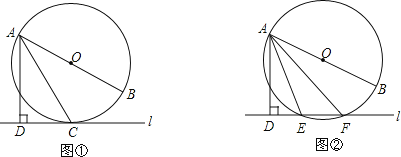
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期,六盘水市教育局组织部分教师分别到A.B.C.D四个地方进行新课程培训,教育局按定额购买了前往四地的车票.如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
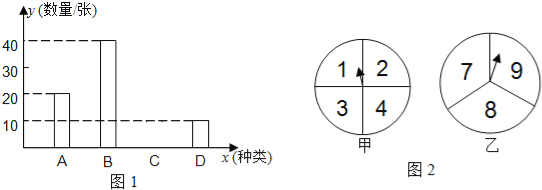
(1)若去C地的车票占全部车票的30%,则去C地的车票数量是 张,补全统计图.
(2)若教育局采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么余老师抽到去B地的概率是多少?
(3)若有一张去A地的车票,张老师和李老师都想要,决定采取旋转转盘的方式来确定.其中甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,如图2所示.具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,票给李老师,否则票给张老师(指针指在线上重转).试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
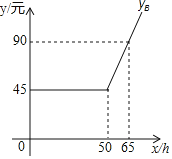
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=![]() ,则△EFC的面积是( )
,则△EFC的面积是( )
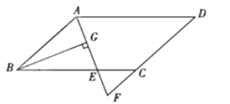
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com