
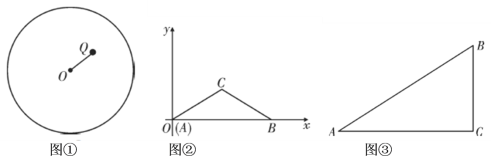
【题目】(1)如图①,圆![]() 的半径为2,圆内有一点
的半径为2,圆内有一点![]() ,
,![]() ,若弦
,若弦![]() 过点
过点![]() ,则弦
,则弦![]() 长度的最大值为______;最小值为______;
长度的最大值为______;最小值为______;
(2)如图②,将![]() 放在如图所示的平面直角坐标系中,点
放在如图所示的平面直角坐标系中,点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .在
.在![]() 轴上方是否存在点
轴上方是否存在点![]() ,使得
,使得![]() ,且
,且![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
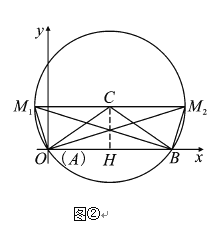
(3)如图③,![]() 是李叔叔家的一块空地示意图,其中
是李叔叔家的一块空地示意图,其中![]() ,
,![]() 米,
米,![]() 米.现在他利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.若李叔叔想建的鱼塘是四边形
米.现在他利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.若李叔叔想建的鱼塘是四边形![]() ,且满足
,且满足![]() ,你认为李叔叔的想法能实现吗?若能,求出这个四边形鱼塘面积和周长的最大值;若不能,请说明理由.
,你认为李叔叔的想法能实现吗?若能,求出这个四边形鱼塘面积和周长的最大值;若不能,请说明理由.
【答案】(1)4,![]() ;(2)存在,坐标为
;(2)存在,坐标为![]() ,
,![]() ;(3)能,这个四边形鱼塘面积最大值为(
;(3)能,这个四边形鱼塘面积最大值为(![]() )平方米,周长的最大值为340米.
)平方米,周长的最大值为340米.
【解析】
(1)当AB为直径时,弦最长;当OP⊥AB时,AB最短,用垂径定理求解即可;
(2)以![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ,过
,过![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于
于![]() ,
,![]() ,点
,点![]() ,
,![]() 即为所求的点;
即为所求的点;
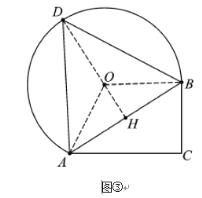
(3)由题意得AB=100,∠ADB=60°,即点D在优弧![]() 上运动,当点D运动到优弧
上运动,当点D运动到优弧![]() 的中点时,四边形鱼塘面积和周长达到最大值,此时
的中点时,四边形鱼塘面积和周长达到最大值,此时![]() 为等边三角形,求出AD和DH长,即可得出这个四边形鱼塘面积和周长的最大值.
为等边三角形,求出AD和DH长,即可得出这个四边形鱼塘面积和周长的最大值.
解:(1)当![]() 为直径时,弦最长,AB=4,
为直径时,弦最长,AB=4,
如图①,当![]() 时,
时,![]() 最短,连接
最短,连接![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
故答案为:4,![]() ;
;
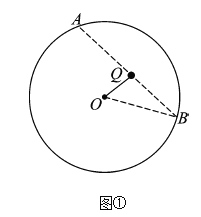
(2)存在,理由如下:
如图②,作![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
以![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() ,
,
过![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于
于![]() ,
,![]() ,
,
则![]() ,且
,且![]() ,
,
![]() 点
点![]() ,
,![]() 符合题意,
符合题意,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 存在点
存在点![]() ,坐标为
,坐标为![]() ,
,![]() ;
;
(3)能,理由如下:如图③,
![]() ,
,![]() 米,
米,![]() 米,
米,
![]() 米.
米.
作![]() ,使得
,使得![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径画
长为半径画![]() ,
,
![]() ,
,
![]() 点
点![]() 在优弧
在优弧![]() 上运动,
上运动,
当点![]() 是优弧
是优弧![]() 的中点时,四边形
的中点时,四边形![]() 面积和周长取得最大值,
面积和周长取得最大值,
连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 这个四边形鱼塘面积最大值为
这个四边形鱼塘面积最大值为![]() (平方米),
(平方米),
这个四边形鱼塘周长的最大值为![]() (米).
(米).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校开发了“书画、器乐、戏曲、棋类”四大类兴趣课程.为了解全校学生对每类课程的选择情况,随机抽取了若干名学生进行调查(每人必选且只能选一类),先将调查结果绘制成如下两幅不完整的统计图:
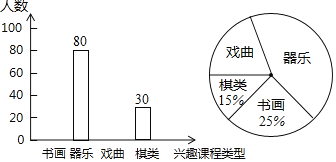
(1)本次随机调查了多少名学生?
(2)补全条形统计图中“书画”、“戏曲”的空缺部分;
(3)若该校共有![]() 名学生,请估计全校学生选择“戏曲”类的人数;
名学生,请估计全校学生选择“戏曲”类的人数;
(4)学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”,用树形图或列表法求处恰好抽到“器乐”和“戏曲”类的概率.(书画、器乐、戏曲、棋类可分别用字幕![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国![]() 周年,东营市某中学决定举办校园艺术节.学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加.为了了解报名情况,组委会在全校随机抽取了若干名学生进行问卷调查,现将报名情况绘制成如图所示的不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
周年,东营市某中学决定举办校园艺术节.学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加.为了了解报名情况,组委会在全校随机抽取了若干名学生进行问卷调查,现将报名情况绘制成如图所示的不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,求“声乐”类对应扇形圆心角的度数;
(4)小东和小颖报名参加“器乐”类比赛,现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器,用列表法或画树状图法求出他们选中同一种乐器的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.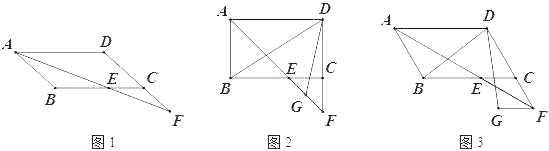
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提升教育教学质量,调动学生学习的兴趣,某校在七年级学生中开展了对语文、数学、英语、历史、地理这五门课程的兴趣爱好情况的调查,以便采取必要教学改革,激发学生对各学科的兴趣爱好.随机选取该年级部分学生进行调查,要求每名学生从中选出一门最感兴趣的课程(每名学生只能选一门,不能多选),以下是根据调查结果绘制的不完整统计图表:
课程代号 |
|
|
|
|
|
课程名称 | 语文 | |数学 | 英语 | 历史 | 地理 |
最感兴趣人数 | 12 | 30 |
| 54 | 9 |
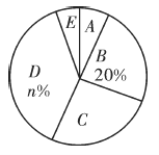
请你根据以上信息,解答下列问题:
(1)被调查学生的总数为______人,![]() ______,
______,![]() ______;
______;
(2)被调查学生中,最喜爱课程的“众数”是______;
(3)若该年级共有800名学生,请估计该年级对语文最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尝试探究
如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() .
.
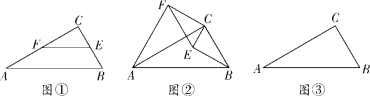
①![]() 的值为________;
的值为________;
②直线![]() 与直线
与直线![]() 的位置关系为________;
的位置关系为________;
(2)类比延伸
如图②,若将图①中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)拓展运用
若![]() ,在旋转过程中,当
,在旋转过程中,当![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提出问题)课间,一位同学拿着方格本遇人便问:“如图所示,在边长为1的小正方形组成的网格中,点A、B、C都是格点,如何证明点A、B、C在同一直线上呢?”

(分析问题)一时间,大家议论开了. 同学甲说:“可以利用代数方法,建立平面直角坐标系,利用函数的知识解决”,同学乙说:“也可以利用几何方法…”同学丙说:“我还有其他的几何证法”……
(解决问题)请你用两种方法解决问题
方法一(用代数方法):

方法二(用几何方法):

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com