
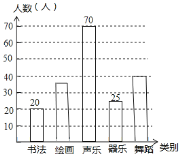
【题目】为庆祝建国![]() 周年,东营市某中学决定举办校园艺术节.学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加.为了了解报名情况,组委会在全校随机抽取了若干名学生进行问卷调查,现将报名情况绘制成如图所示的不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
周年,东营市某中学决定举办校园艺术节.学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加.为了了解报名情况,组委会在全校随机抽取了若干名学生进行问卷调查,现将报名情况绘制成如图所示的不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,求“声乐”类对应扇形圆心角的度数;
(4)小东和小颖报名参加“器乐”类比赛,现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器,用列表法或画树状图法求出他们选中同一种乐器的概率.

【答案】(1)200人;![]() “绘画”:35人,“舞蹈”:50人;
“绘画”:35人,“舞蹈”:50人;![]()
![]() ;
;![]()
![]()
【解析】
(1)根据统计图可得报名“书法”类的人数有![]() 人,占整个被抽取到学生总数的
人,占整个被抽取到学生总数的![]() ,再进行计算即可得到答案;
,再进行计算即可得到答案;
(2)根据统计图可以报名“绘画”类的人数,从而报名“舞蹈”类的人数,则可以将条形统计图补充完整;
(3)由报名“声乐”类的人数为![]() 人,可得“声乐”类对应扇形圆心角的度数;
人,可得“声乐”类对应扇形圆心角的度数;
(4)根据树状图进行求解即可得到答案.
解:![]() 被抽到的学生中,报名“书法”类的人数有
被抽到的学生中,报名“书法”类的人数有![]() 人,
人,
占整个被抽取到学生总数的![]() ,
,
![]() 在这次调查中,一共抽取了学生为:
在这次调查中,一共抽取了学生为:![]() (人);
(人);
![]() 被抽到的学生中,报名“绘画”类的人数为:
被抽到的学生中,报名“绘画”类的人数为:![]() (人),
(人),
报名“舞蹈”类的人数为:![]() (人);
(人);
补全条形统计图如下:
![]() 被抽到的学生中,报名“声乐”类的人数为
被抽到的学生中,报名“声乐”类的人数为![]() 人,
人,
![]() 扇形统计图中,“声乐”类对应扇形圆心角的度数为:
扇形统计图中,“声乐”类对应扇形圆心角的度数为:![]() ;
;
![]() 设小提琴、单簧管、钢琴、电子琴四种乐器分别为
设小提琴、单簧管、钢琴、电子琴四种乐器分别为![]() ,
,
画树状图如图所示:
共有![]() 个等可能的结果,小东和小颖选中同一种乐器的结果有
个等可能的结果,小东和小颖选中同一种乐器的结果有![]() 个,
个,
![]() 小东和小颖选中同一种乐器的概率为
小东和小颖选中同一种乐器的概率为![]() .
.
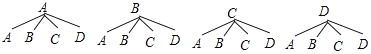


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,这四张纸牌背面朝上洗匀.
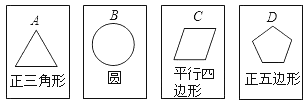
(1)从中随机摸出一张,求摸出的牌正面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则如下:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌正面图形都是轴对称图形,则小明获胜,否则小亮获胜,这个游戏公平吗?请用列表或画树状图的方法说明. (纸牌用![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D是边BC上一动点,连接AD,过点A作AE⊥AD,且AE=AD,连接CE.

(1)如图,求证:BD=CE;
(2)若AF平分∠DAE交直线BC于点F.
①如图,当点F在线段BC上,猜想线段BD,DF,FC之间的数量关系,并证明;
②若BD=6,CF=8,直接写出AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=6,对角线AC和BD相交于点O,E是AB所在直线上一点(不与点B重合),将线段OE绕点E顺时针旋转90°得到EF.
(1)如图1,当点E和点A重合时,连接BF,直接写出BF的长为 ;
(2)如图2,点E在线段AB上,且AE=1,连接BF,求BF的长;
(3)若DG:AG=2:1,连接CF,H是CF的中点,是否存在点E使△GEH是以EG为直角边的直角三角形?若存在,请直接写出EB的长;若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
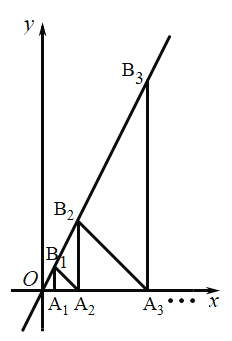
【题目】如图,在坐标轴上取点![]() ,作
,作![]() 轴的垂线与直线
轴的垂线与直线![]() 交于点
交于点![]() ,作等腰直角三角形
,作等腰直角三角形![]() ;又过点
;又过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 交于点
交于点![]() ,作等腰直角三角形
,作等腰直角三角形![]() ,如此反复作等腰直角三角形,当作到
,如此反复作等腰直角三角形,当作到![]() 点时,点
点时,点![]() 的坐标是_____________
的坐标是_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
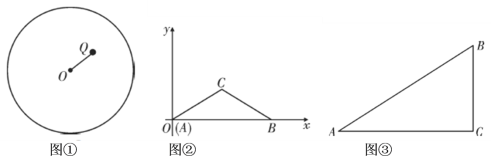
【题目】(1)如图①,圆![]() 的半径为2,圆内有一点
的半径为2,圆内有一点![]() ,
,![]() ,若弦
,若弦![]() 过点
过点![]() ,则弦
,则弦![]() 长度的最大值为______;最小值为______;
长度的最大值为______;最小值为______;
(2)如图②,将![]() 放在如图所示的平面直角坐标系中,点
放在如图所示的平面直角坐标系中,点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .在
.在![]() 轴上方是否存在点
轴上方是否存在点![]() ,使得
,使得![]() ,且
,且![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图③,![]() 是李叔叔家的一块空地示意图,其中
是李叔叔家的一块空地示意图,其中![]() ,
,![]() 米,
米,![]() 米.现在他利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.若李叔叔想建的鱼塘是四边形
米.现在他利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.若李叔叔想建的鱼塘是四边形![]() ,且满足
,且满足![]() ,你认为李叔叔的想法能实现吗?若能,求出这个四边形鱼塘面积和周长的最大值;若不能,请说明理由.
,你认为李叔叔的想法能实现吗?若能,求出这个四边形鱼塘面积和周长的最大值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com