
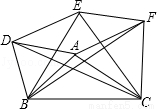
以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.
(1)请猜想四边形ADEF是什么特殊四边形?并说明理由.
(2)当△ABC满足条件___________时,四边形ADEF为矩形;
(3) 当△ABC满足条件___________时,四边形ADEF不存在.

(1) 四边形ADEF是平行四边形,证明见解析;
(2)∠BAC=150°;
(3)∠BAC=60°.
【解析】
试题分析:(1)可先证明△ABC≌△DBE,可得DE=AC,又有AC=AF,可得DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;
(2)如四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;
(3)根据∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
试题解析:(1)四边形ADEF是平行四边形;
∵△ABD,△BCE都是等边三角形,
∴∠DBE=∠ABC=60°﹣∠ABE,AB=BD,BC=BE.
在△ABC和△DBE中,
 ,
,
∴△ABC≌△DBE(SAS).
∴DE=AC.
又∵AC=AF,
∴DE=AF.
同理可得EF=AD.
∴四边形ADEF是平行四边形;
(2)∵四边形ADEF是平行四边形,
∴当∠DAF=90°时,四边形ADEF是矩形,
∴∠FAD=90°.
∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°.
则当∠BAC=150°时,四边形ADEF是矩形;
(3)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
 .
.
考点:1.矩形的判定2.全等三角形的判定与性质3.等边三角形的性质4.平行四边形的判定.


科目:初中数学 来源:2015届江苏省常熟市八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,点A、B在反比例函数y=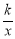 (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为 .
(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为 .

查看答案和解析>>
科目:初中数学 来源:2015届江苏省兴化市八年级下学期期中考试数学试卷(解析版) 题型:选择题
下列说法中,错误的是( )
A.平行四边形的对角线互相平分
B.菱形的对角线互相垂直
C.矩形的对角线相等
D.正方形的对角线不一定互相平分
查看答案和解析>>
科目:初中数学 来源:2015届江苏无锡市八年级下学期期中考试数学卷(解析版) 题型:解答题
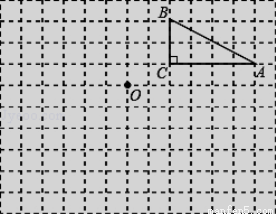
如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC绕点C顺时针旋转 得到△A1B1C1;
得到△A1B1C1;
(2)作△ABC关于点O成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源:2015届江苏无锡市八年级下学期期中考试数学卷(解析版) 题型:填空题
下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确的命题是_________________(将命题的序号填上即可).
查看答案和解析>>
科目:初中数学 来源:2015届江苏无锡前洲中学八年级3月阶段练习数学试卷(解析版) 题型:解答题
在平行四边形 中,
中,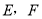 分别为边
分别为边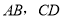 的中点,连接
的中点,连接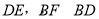 .
.

(1)求证: .(4分)
.(4分)
(2)若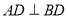 ,则四边形
,则四边形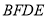 是什么特殊四边形?请证明你的结论.(5分)
是什么特殊四边形?请证明你的结论.(5分)
查看答案和解析>>
科目:初中数学 来源:2015届江苏宜兴和桥学区八年级下学期期中考试数学试卷(解析版) 题型:选择题
“清明”期间,几名同学包租一辆面包车前往“宜兴竹海”游玩,面包车的租价为600元,出发时,又增加了4名学生,结果每个同学比原来少分担25元车费,设原来参加游玩的同学为x人,则可得方程 ( )
A.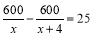 B.
B.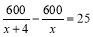
C.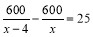 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com